RKToolbox Guide
Mario Berljafa, Steven Elsworth, and Stefan Güttel (The University of Manchester, UK)
Overview
Thank you for your interest in the Rational Krylov Toolbox (RKToolbox). The RKToolbox is a collection of scientific computing tools based on rational Krylov techniques. The development started in 2013 and the current version 2.9 (released in 2020) provides
- an implementation of Ruhe's (block) rational Krylov sequence method [2, 5, 9, 10], allowing to control various options, including user-defined inner products, exploitation of complex-conjugate shifts, orthogonalization, rerunning [3], and simulated parallelism [4],
- algorithms for the implicit and explicit relocation of the poles of a rational Krylov space [2],
- a collection of utility functions and a gallery of special rational functions (e.g., Zolotarev approximants),
- an implementation of RKFIT [2, 3], a robust algorithm for approximate rational least squares approximation, including automated degree reduction,
- the RKFUN class [3] for numerical computations with rational functions, including support for MATLAB Variable Precision Arithmetic and the Advanpix Multiple Precision toolbox [1],
- the RKFUNM class, a matrix-valued generalization of RKFUNs, together with the ability to sample and solve nonlinear eigenvalue problems using the NLEIGS [7] and AAA algorithms [8], and
- the RKFUNB and BARYFUN classes [5] for numerical computations with more general rational matrix-valued formats.
This guide explains the main functionalities of the toolbox. To run the embedded MATLAB codes the RKToolbox needs to be in MATLAB's search path. For details about the installation we refer to the Download section on http://rktoolbox.org/.
Click here to view the PDF version of this guide.
Rational Krylov spaces
A (single-vector) rational Krylov space is a linear vector space of rational functions in a matrix times a vector. Let 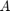 be a square matrix of size
be a square matrix of size  ,
, 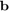 an
an 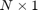 starting vector, and let
starting vector, and let 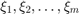 be a sequence of complex or infinite poles all distinct from the eigenvalues of
be a sequence of complex or infinite poles all distinct from the eigenvalues of 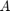 . Then the rational Krylov space of order
. Then the rational Krylov space of order 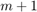 associated with
associated with 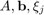 is defined as
is defined as
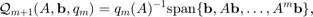
where 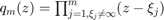 is the common denominator of the rational functions associated with the rational Krylov space. The rational Krylov method by Ruhe [9, 10] computes an orthonormal basis
is the common denominator of the rational functions associated with the rational Krylov space. The rational Krylov method by Ruhe [9, 10] computes an orthonormal basis 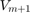 of
of 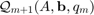 . The basis matrix
. The basis matrix  satisfies a rational Arnoldi decomposition of the form
satisfies a rational Arnoldi decomposition of the form
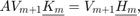
where 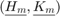 is an (unreduced) upper Hessenberg pencil of size
is an (unreduced) upper Hessenberg pencil of size 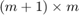 .
.
Rational Arnoldi decompositions are useful for several purposes. For example, the eigenvalues of the upper 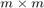 part of the pencil
part of the pencil 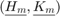 can be excellent approximations to some of
can be excellent approximations to some of 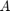 's eigenvalues [9, 10]. Other applications include matrix function approximation and rational quadrature, model order reduction, matrix equations, nonlinear eigenproblems, and rational least squares fitting (RKFIT).
's eigenvalues [9, 10]. Other applications include matrix function approximation and rational quadrature, model order reduction, matrix equations, nonlinear eigenproblems, and rational least squares fitting (RKFIT).
Computing rational Krylov bases
Relevant functions: rat_krylov, util_cplxpair
Let us compute 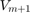 ,
, 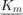 , and
, and  using the rat_krylov function, and verify that the outputs satisfy the rational Arnoldi decomposition by computing the relative residual norm
using the rat_krylov function, and verify that the outputs satisfy the rational Arnoldi decomposition by computing the relative residual norm  . For
. For 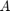 we take the tridiag matrix of size
we take the tridiag matrix of size 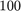 from MATLAB's gallery, and
from MATLAB's gallery, and ![$\mathbf{b} = [1,0,\ldots,0]^T$](guide_eq10588513863987664463.png) . The
. The 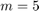 poles
poles 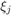 are, in order,
are, in order, 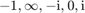 .
.
N = 100; % matrix size A = gallery('tridiag', N); b = eye(N, 1); % starting vector xi = [-1, inf, -1i, 0, 1i]; % m = 5 poles [V, K, H] = rat_krylov(A, b, xi); resnorm = norm(A*V*K - V*H)/norm(H) % residual check
resnorm = 3.5143e-16
As some of the poles 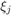 in this example are complex, the matrices
in this example are complex, the matrices 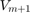 ,
, 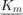 , and
, and  are complex, too:
are complex, too:
disp([isreal(V), isreal(K), isreal(H)])
0 0 0
However, the poles 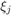 can be reordered using the function util_cplxpair so that complex-conjugate pairs appear next to each other. After reordering the poles, we can call the function rat_krylov with the 'real' option, thereby computing a real-valued rational Arnoldi decomposition [9].
can be reordered using the function util_cplxpair so that complex-conjugate pairs appear next to each other. After reordering the poles, we can call the function rat_krylov with the 'real' option, thereby computing a real-valued rational Arnoldi decomposition [9].
% Group together poles appearing in complex-conjugate pairs. xi = util_cplxpair(xi); [V, K, H] = rat_krylov(A, b, xi, 'real'); resnorm = norm(A*V*K - V*H)/norm(H) disp([isreal(V), isreal(K), isreal(H)])
resnorm =
3.8874e-16
1 1 1
Block rational Krylov spaces
A block Krylov space is a linear space of block vectors of size 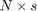 built with a matrix
built with a matrix 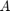 of size
of size 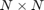 and a starting block vector
and a starting block vector ![$\mathbf{b} = [b_1, b_2, \ldots, b_s]$](guide_eq06187549497977120977.png) of size
of size 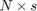 , with maximal rank. Let
, with maximal rank. Let 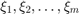 be a sequence of complex or infinite poles all distinct from the eigenvalues of
be a sequence of complex or infinite poles all distinct from the eigenvalues of 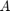 . Then the block rational Krylov space of order
. Then the block rational Krylov space of order 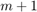 associated with
associated with 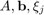 is defined as
is defined as
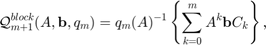
where 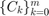 are matrices of size
are matrices of size  and
and 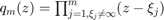 is the common denominator of the rational matrix-valued functions associated with the block rational Krylov space. The block rational Arnoldi method [5] produces an orthonormal block matrix
is the common denominator of the rational matrix-valued functions associated with the block rational Krylov space. The block rational Arnoldi method [5] produces an orthonormal block matrix ![$\mathbf{V}_{m+1} = [\mathbf{v}_1, \ldots, \mathbf{v}_{m+1}]$](guide_eq11307978229621366596.png) of size
of size 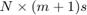 which satisfies a block rational Arnoldi decomposition of the form
which satisfies a block rational Arnoldi decomposition of the form
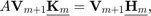
where 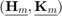 is an (unreduced) block upper Hessenberg matrix pencil of size
is an (unreduced) block upper Hessenberg matrix pencil of size 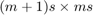 . The block vectors in
. The block vectors in 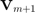 blockspan the space
blockspan the space 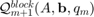 , that is
, that is
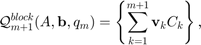
where the 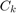 are arbitrary matrices of size
are arbitrary matrices of size  .
.
Block rational Krylov spaces have applications in eigenproblems with repeated eigenvalues, model order reduction, matrix equations, and for solving parameterized linear systems with multiple right-hand sides as they arise, for example, in multisource electromagnetic modelling.
Computing block rational Krylov bases
Relevant functions: rat_krylov
Let us compute 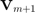 ,
, 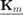 , and
, and  using the rat_krylov function, and verify that the outputs satisfy the rational Arnoldi decomposition by computing the relative residual norm
using the rat_krylov function, and verify that the outputs satisfy the rational Arnoldi decomposition by computing the relative residual norm 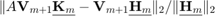 , and check the orthogonality by computing
, and check the orthogonality by computing  .
.
N = 100; % matrix size A = gallery('tridiag', N); b = zeros(N, 2); b(1,1) = 1; b(7,2) = 1; xi = [-1, inf, -1i, 0, 1i]; % m = 5 poles [V, K, H] = rat_krylov(A, b, xi); resnorm = norm(A*V*K - V*H)/norm(H) % residual check orthnorm = norm(V'*V - eye(size(V,2))) % orthogonality check
resnorm = 4.1343e-16 orthnorm = 6.6608e-16
The rat_krylov function also has the ability to extend the space with additional poles. When extending a block rational Krylov space, you must specify  , the block size, as there is no way to infer
, the block size, as there is no way to infer  from the existing decomposition. This is done using the parameter param.extend.
from the existing decomposition. This is done using the parameter param.extend.
param.deflation_tol = eps(1); % default deflation tolerance param.extend = 2; % block size s, 1 by default xi = 1; [V1, K1, H1] = rat_krylov(A, V, K, H, xi, param); resnorm = norm(A*V1*K1 - V1*H1)/norm(H1) % residual check orthnorm = norm(V1'*V1 - eye(size(V1,2))) % orthogonality check
resnorm = 4.2754e-16 orthnorm = 1.2369e-04
The loss of orthogonality occured as the columns of 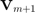 become nearly linearly dependent. Removing the nearly linearly dependent vectors is called deflation. At each iteration, the block rational Arnoldi method uses an economy-size QR factorization with pivoting to detect (near) rank deficiencies. The deflation tolerance can be controlled by the parameter param.deflation_tol.
become nearly linearly dependent. Removing the nearly linearly dependent vectors is called deflation. At each iteration, the block rational Arnoldi method uses an economy-size QR factorization with pivoting to detect (near) rank deficiencies. The deflation tolerance can be controlled by the parameter param.deflation_tol.
param.deflation_tol = 1e-10; % increase deflation tolerance param.extend = 2; xi = 1; [V2, K2, H2, out] = rat_krylov(A, V, K, H, xi, param); resnorm = norm(A*V2*K2 - V2*H2)/norm(H2) % residual check orthnorm = norm(V2'*V2 - eye(size(V2,2))) % orthogonality check
Warning: rat_krylov: 1 column deflated resnorm = 6.0479e-14 orthnorm = 6.6385e-16
Removing the linearly dependent columns from 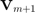 results in an uneven block structure of the rational Arnoldi decomposition, but the orthogonality check has now passed. The residual norm has increased as the upper-Hessenberg matrix pencil still has columns containing information about the deflated vectors. Removing the corresponding columns from the pencil gives a so-called thin decomposition [5].
results in an uneven block structure of the rational Arnoldi decomposition, but the orthogonality check has now passed. The residual norm has increased as the upper-Hessenberg matrix pencil still has columns containing information about the deflated vectors. Removing the corresponding columns from the pencil gives a so-called thin decomposition [5].
K2thin = K2(:,out.column_deflation);
H2thin = H2(:, out.column_deflation);
resnorm = norm(A*V2*K2thin - V2*H2thin)/norm(H2thin) % residual check
resnorm = 4.1351e-16
Our implementation rat_krylov supports many features not shown in the basic description above.
- It is possible to use matrix pencils
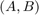 instead of a single matrix
instead of a single matrix 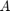 . This leads to decompositions of the form
. This leads to decompositions of the form 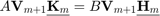 .
. - Both the matrix
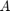 and the pencil
and the pencil 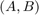 can be passed either explicitly, or implicitly by providing function handles to perform matrix-vector products and to solve shifted linear systems.
can be passed either explicitly, or implicitly by providing function handles to perform matrix-vector products and to solve shifted linear systems. - Non-standard inner products for constructing the orthonormal bases are supported.
- One can choose between classical (CGS) and modified Gram-Schmidt orthogonalisation with or without reorthogonalization.
- Iterative refinement for the linear system solves is supported.
For more details type help rat_krylov.
Moving poles of a rational Krylov space
Relevant functions: move_poles_expl, move_poles_impl
There is a direct link between the starting vector 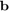 and the poles
and the poles 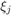 of a rational Krylov space
of a rational Krylov space 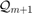 . A change of the poles
. A change of the poles 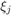 to
to  can be interpreted as a change of the starting vector from
can be interpreted as a change of the starting vector from 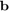 to
to  , and vice versa. Algorithms for moving the poles of a rational Krylov space are described in [2] and implemented in the functions move_poles_expl and move_poles_impl.
, and vice versa. Algorithms for moving the poles of a rational Krylov space are described in [2] and implemented in the functions move_poles_expl and move_poles_impl.
Example: Let us move the 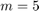 poles
poles 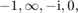 and
and  into
into 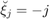 ,
, 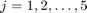 .
.
N = 100;
A = gallery('tridiag', N);
b = eye(N, 1);
xi = [-1, inf, -1i, 0, 1i];
[V, K, H] = rat_krylov(A, b, xi);
xi_new = -1:-1:-5;
[KT, HT, QT, ZT] = move_poles_expl(K, H, xi_new);
The poles of a rational Krylov space are the eigenvalues of the lower 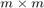 part of the pencil
part of the pencil 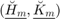 in a rational Arnoldi decomposition
in a rational Arnoldi decomposition 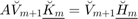 associated with that space [2]. By transforming a rational Arnoldi decomposition we are therefore effectively moving the poles:
associated with that space [2]. By transforming a rational Arnoldi decomposition we are therefore effectively moving the poles:
VT = V*QT'; resnorm = norm(A*VT*KT - VT*HT)/norm(HT) moved_poles = util_pencil_poles(KT, HT).'
resnorm = 6.8004e-16 moved_poles = -1.0000e+00 + 1.1140e-16i -2.0000e+00 + 1.4085e-15i -3.0000e+00 - 7.2486e-16i -4.0000e+00 + 1.6407e-16i -5.0000e+00 - 2.4095e-16i
Rational Krylov fitting (RKFIT)
Relevant function: rkfit
RKFIT [2, 3] is an iterative Krylov-based algorithm for nonlinear rational approximation. Given two families of  matrices
matrices ![$\{F^{[j]}\}_{j=1}^{\ell}$](guide_eq11228717829556212653.png) and
and ![$\{D^{[j]}\}_{j=1}^{\ell}$](guide_eq08383534074473232374.png) , an
, an 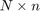 block of vectors
block of vectors 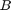 , and an
, and an  matrix
matrix 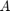 , the algorithm seeks a family of rational functions
, the algorithm seeks a family of rational functions ![$\lbrace r^{[j]} \rbrace_{j=1}^{\ell}$](guide_eq04089485158783793701.png) of type
of type 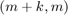 , all sharing a common denominator
, all sharing a common denominator  , such that the relative misfit
, such that the relative misfit
![$$\displaystyle {\rm misfit} = \sqrt{\frac{{\sum_{j=1}^\ell \| D^{[j]} [ F^{[j]}B - r^{[j]}(A)B ] \|_F^2}}{{\sum_{j=1}^\ell \| D^{[j]} F^{[j]} B \|_F^2}}}\to\min$$](guide_eq03928207865650854707.png)
is minimal. The matrices ![$\{D^{[j]}\}_{j=1}^{\ell}$](guide_eq08383534074473232374.png) are optional, and if not provided
are optional, and if not provided ![$D^{[j]}=I_N$](guide_eq01979618813957681495.png) is assumed. The algorithm takes an initial guess for
is assumed. The algorithm takes an initial guess for  and iteratively tries to improve it by relocating the poles of a rational Krylov space.
and iteratively tries to improve it by relocating the poles of a rational Krylov space.
We now show on a simple example how to use the rkfit function. Consider again the tridiagonal matrix 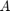 and the vector
and the vector 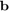 from above and let
from above and let 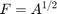 .
.
N = 100;
A = gallery('tridiag', N);
b = eye(N, 1);
F = sqrtm(full(A));
exact = F*b;
Now let us find a rational function  of type
of type 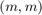 with
with  such that
such that 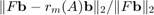 is small. The function rkfit requires an input vector of
is small. The function rkfit requires an input vector of  initial poles and then tries to return an improved set of poles. If we had no clue about where to place the initial poles we can easily set them all to infinity. In the following we run RKFIT for at most
initial poles and then tries to return an improved set of poles. If we had no clue about where to place the initial poles we can easily set them all to infinity. In the following we run RKFIT for at most 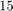 iterations and aim at relative misfit
iterations and aim at relative misfit 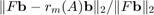 below
below 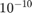 . We display the error after each iteration.
. We display the error after each iteration.
[xi, ratfun, misfit] = rkfit(F, A, b, ... repmat(inf, 1, 10), ... 15, 1e-10, 'real'); disp(misfit)
7.1549e-07 1.4504e-10 4.6348e-11
The rational function  of type
of type 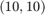 approximates
approximates  to about
to about 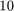 decimal places. A useful output of rkfit is the RKFUN object ratfun representing the rational function
decimal places. A useful output of rkfit is the RKFUN object ratfun representing the rational function 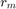 . It can be used, for example, to evaluate
. It can be used, for example, to evaluate  :
:
- ratfun(A,v) evaluates
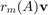 as a matrix function times a vector,
as a matrix function times a vector, - ratfun(A,V) evaluates
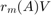 as a matrix function times a matrix, e.g., setting
as a matrix function times a matrix, e.g., setting 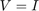 as the identity matrix will return the full matrix function
as the identity matrix will return the full matrix function 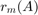 , or
, or - ratfun(z) evaluates
 as a scalar function in the complex plane.
as a scalar function in the complex plane.
Here is a plot of the error  over the spectral interval of
over the spectral interval of 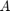 (approximately
(approximately ![$[0,4]$](guide_eq06167377142463551117.png) ), together with the values at the eigenvalues of
), together with the values at the eigenvalues of 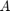 :
:
figure ee = eig(full(A)).'; xx = sort([logspace(-4.3, 1, 500) , ee]); loglog(xx,abs(sqrt(xx) - ratfun(xx))); hold on loglog(ee,abs(sqrt(ee) - ratfun(ee)), 'r.', 'markers', 15) axis([4e-4, 8, 1e-14, 1e-3]); xlabel('x'); grid on title('| x^{1/2} - r_m(x) |','interpreter','tex')
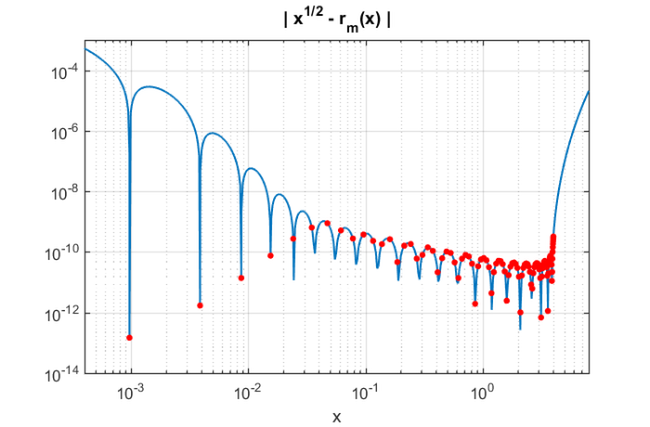
As expected the rational function  is a good approximation of the square root over
is a good approximation of the square root over ![$[0,4]$](guide_eq06167377142463551117.png) . It is, however, not a uniform approximation because we are approximately minimizing the 2-norm error on the eigenvalues of
. It is, however, not a uniform approximation because we are approximately minimizing the 2-norm error on the eigenvalues of 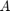 , and moreover we are implicitly using a weight function given by the components of
, and moreover we are implicitly using a weight function given by the components of 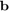 in
in 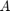 's eigenvector basis.
's eigenvector basis.
Additional features of RKFIT are listed below.
- An automated degree reduction procedure [3, Section 4] is implemented; it takes place if a relative misfit below tolerance is achieved, unless deactivated.
- Nondiagonal rational approximants are supported; they can be specified via an additional param structure.
- Adaptive incrementation of the degree controlled by a tolerance when an empty set of poles xi is provided.
- Utility functions are provided for transforming scalar data appearing in complex-conjugate pairs into real-valued data, as explained in [3, Section 3.5].
For more details type help rkfit.
Some of the capabilities of RKFUN are shown in the following section.
The RKFUN class
RKFUN is the fundamental data type to represent and work with rational functions. It has already been described above how to evaluate an RKFUN object ratfun for scalar or matrix arguments by calling ratfun(z) or ratfun(A,v), respectively. There are more than 30 RKFUN methods implemented, and a list of these can be obtained by typing methods rkfun:
basis - Orthonormal rational basis functions of an RKFUN. coeffs - Expansion coefficients of an RKFUN. contfrac - Convert an RKFUN into continued fraction form. diff - Differentiate an RKFUN. disp - Display information about an RKFUN. double - Convert an RKFUN into double precision (undo vpa or mp). ezplot - Easy-to-use function plotter for RKFUNs. feval - Evaluate an RKFUN at scalar or matrix arguments. hess - Convert an RKFUN pencil to (strict) upper-Hessenberg form. inv - Invert an RKFUN corresponding to a Moebius transform. isreal - Returns true if an RKFUN is real-valued. minus - Scalar subtraction. mp - Convert an RKFUN into Advanpix Multiple Precision format. mrdivide - Scalar division. mtimes - Scalar multiplication. plus - Scalar addition. poles - Return the poles of an RKFUN. poly - Convert an RKFUN into a quotient of two polynomials. power - Integer exponentiation of an RKFUN. rdivide - Division of two RKFUN. residue - Convert an RKFUN into partial fraction form. rkfun - The RKFUN constructor. roots - Compute the roots of an RKFUN. size - Returns the size of an RKFUN. subsref - Evaluate an RKFUN (calls feval). times - Multiplication of two RKFUNs. type - Return the type (m+k,m) of an RKFUN. uminus - Unary minus. uplus - Unary plus. vpa - Convert RKFUN into MATLAB's variable precision format.
The names of these methods should be self-explanatory. For example, roots(ratfun) will return the roots of ratfun, and residue(ratfun) will compute its partial fraction form. Most methods support the use of MATLAB's Variable Precision Arithmetic (VPA) and, preferably, the Advanpix Multiple Precision toolbox (MP)[1]. So, for example, contfrac(mp(ratfun)) will compute a continued fraction expansion of ratfun using multiple precision arithmetic. For more details on each of the methods, type help rkfun.<method name>.
The RKFUN gallery provides some predefined rational functions that may be useful. A list of the options can be accessed as follows:
help rkfun.gallery
GALLERY Collection of rational functions.
obj = rkfun.gallery(funname, param1, param2, ...) takes
funname, a case-insensitive string that is the name of
a rational function family, and the family's input
parameters.
See the listing below for available function families.
constant Constant function of value param1.
cheby Chebyshev polynomial (first kind) of degree param1.
cayley Cayley transformation (1-z)/(1+z).
moebius Moebius transformation (az+b)/(cz+d) with
param1 = [a,b,c,d].
sqrt Zolotarev sqrt approximation of degree param1 on
the positive interval [1,param2].
invsqrt Zolotarev invsqrt approximation of degree param1 on
the positive interval [1,param2].
sqrt0h balanced Remez approximation to sqrt(x+(h*x/2)^2)
of degree param3 on [param1,param2],
where param1 <= 0 <= param2 and h = param4.
sqrt2h balanced Zolotarev approximation to sqrt(x+(hx/2)^2)
of degree param5 on [param1,param2]U[param3,param4],
param1 < param2 < 0 < param3 < param4, h = param6.
invsqrt2h balanced Zolotarev approximation to 1/sqrt(x+(hx/2)^2)
of degree param5 on [param1,param2]U[param3,param4],
param1 < param2 < 0 < param3 < param4, h = param6.
sign Zolotarev sign approximation of degree 2*param1 on
the union of [1,param2] and [-param2,-1].
step Unit step function approximation for [-1,1] of
degree 2*param1 with steepness param2.
Another way to create an RKFUN is to make use of MATLAB's symbolic engine. For example, r = rkfun('(x+1)*(x-2)/(x-3)^2') returns a rational function as expected. Alternatively, one can specify a rational function by its roots and poles (and an optional scaling factor) using the rkfun.nodes2rkfun function. For example, r = rkfun.nodes2rkfun([-1,2],[3,3]) will create the same rational function as above. One can also specify a rational interpolant by its barycentric representation; see the function util_bary2rkfun and reference [6].
The RKFUNM class
The RKFUNM class is the matrix-valued generalization of RKFUN. RKFUNM objects are mainly generated via the util_nleigs and util_aaa sampling routines for nonlinear eigenvalue problems. The class provides a method called linearize, which returns a matrix pencil structure corresponding to a linearization of the RKFUNM. This pencil can be used in combination with the rat_krylov function for finding eigenvalues of the linearization.
We illustrate the capabilities of the RKFUNM class with the help of a simple example. Assume we want to find numbers  in the interval
in the interval ![$[-\pi,\pi]$](guide_eq04277113708218156659.png) where the
where the  matrix
matrix 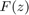 defined below becomes singular:
defined below becomes singular:
F = @(z) [ sin(5*z) , 1 ; 1 , 1 ];
With the help of the AAA algorithm [8] we sample this matrix at sufficiently many points in the search interval and construct an accurate rational interpolant, which is then converted into RKFUNM format; see [6] for details on the conversion:
Z = linspace(-pi,pi,500); ratm = util_aaa(F,Z)
ratm = RKFUNM object of size 2-by-2 and type (21, 21). Real dense coefficient matrices of size 2-by-2. Real-valued Hessenberg pencil (H, K) of size 22-by-21.
We see that ratm is indeed an RKFUNM object representing a matrix-valued rational function of degree 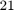 . In order to solve the nonlinear eigenvalue problem
. In order to solve the nonlinear eigenvalue problem 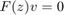 ,
, 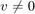 , we have to linearize ratm and find the eigenvalues of the linearization near the search interval:
, we have to linearize ratm and find the eigenvalues of the linearization near the search interval:
AB = linearize(ratm); [A,B] = AB.get_matrices(); evs = eig(full(A), full(B)); evs = evs(abs(imag(evs))< 1e-7 & abs(evs)<pi); figure; plot(Z,sin(5*Z)); hold on; h2 = plot(real(evs),0*evs + 1,'ro'); legend('sin(5z)','eigenvalues','Location','SouthEast')
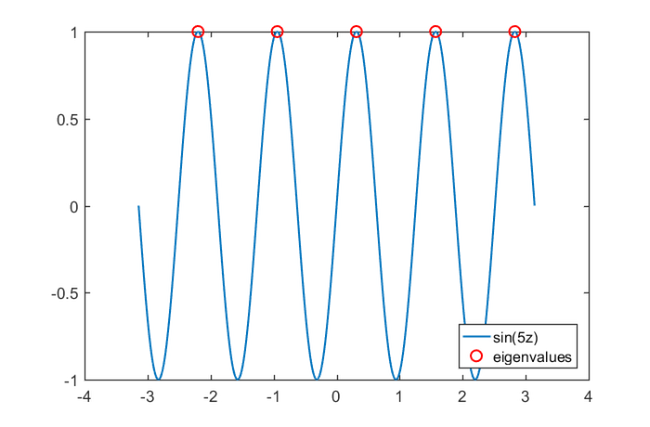
Indeed, the solutions of  are the points where
are the points where 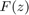 becomes singular. For linearizations of larger dimension the pencil AB should not be converted into matrix form using AB.get_matrices(). Instead, AB should be used as input to rat_krylov for solving the linear eigenvalue problem iteratively:
becomes singular. For linearizations of larger dimension the pencil AB should not be converted into matrix form using AB.get_matrices(). Instead, AB should be used as input to rat_krylov for solving the linear eigenvalue problem iteratively:
xi = zeros(1,30); % poles of the Krylov space [m,n] = type(ratm); dimlin = m*size(ratm,1); % dimension of linearization rng(0), v = randn(dimlin, 1); % starting vector of Krylov space [V, K, H] = rat_krylov(AB, v, xi); ritzval = eig(H(1:end-1, :), K(1:end-1, :)); % Ritz values ritzval = ritzval(abs(imag(ritzval))< 1e-14 & abs(ritzval)<pi); plot(ritzval, 0*ritzval + 1, 'g*'); legend('sin(5z)','eigenvalues',... 'Ritz values','Location','SouthEast')

The RKFUNB class
RKFUNB is a data type to represent rational matrix-valued functions of the form
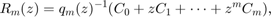
where 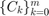 are matrices of size
are matrices of size  . The vectors computed by the block version of the rational Arnoldi method are closely linked with such functions. RKFUNBs
. The vectors computed by the block version of the rational Arnoldi method are closely linked with such functions. RKFUNBs 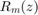 can be evaluated as follows:
can be evaluated as follows:
- R(A,v) evaluates
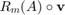 as a rational matrix-valued function circed with a block vector, that is,
as a rational matrix-valued function circed with a block vector, that is, 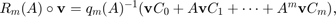
- R(z) evaluates
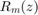 at a scalar argument, giving a matrix of size
at a scalar argument, giving a matrix of size  .
.
See [5] for more details.
References
[1] Advanpix LLC., Multiprecision Computing Toolbox for MATLAB, version 4.3.3.12213, Tokyo, Japan, 2017. http://www.advanpix.com/.
[2] M. Berljafa and S. Güttel. Generalized rational Krylov decompositions with an application to rational approximation, SIAM J. Matrix Anal. Appl., 36(2):894--916, 2015.
[3] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[4] M. Berljafa and S. Güttel. Parallelization of the rational Arnoldi algorithm, SIAM J. Sci. Comput., 39(5):S197--S221, 2017.
[5] S. Elsworth and S. Güttel. The block rational Arnoldi method, SIAM J. Matrix Anal. Appl., 41(2):365--388, 2020.
[6] S. Elsworth and S. Güttel. Conversions between barycentric, RKFUN, and Newton representations of rational interpolants, Linear Algebra Appl., 576:246--257, 2019.
[7] S. Güttel, R. Van Beeumen, K. Meerbergen, and W. Michiels. NLEIGS: A class of fully rational Krylov methods for nonlinear eigenvalue problems, SIAM J. Sci. Comput., 36(6):A2842--A2864, 2014.
[8] Y. Nakatsukasa, O. Sète, and L. N. Trefethen. The AAA algorithm for rational approximation, SIAM J. Sci. Comput., 40(3):A1494--A1522, 2018.
[9] A. Ruhe. Rational Krylov: A practical algorithm for large sparse nonsymmetric matrix pencils, SIAM J. Sci. Comput., 19(5):1535--1551, 1998.
[10] A. Ruhe. The rational Krylov algorithm for nonsymmetric eigenvalue problems. III: Complex shifts for real matrices, BIT, 34:165--176, 1994.