An overview of the example collection
Mario Berljafa, Steven Elsworth, Stefan GüttelDownload PDF or m-file
Contents
Welcome
Welcome to this example collection, which intends to demonstrate some of the features of the MATLAB Rational Krylov Toolbox. Simply use the menu on the left-hand side to navigate through the collection. Each example is available as a MATLAB m-file and in PDF format (see the links in the above header). All examples are also included in the rktoolbox.zip file available from the RKToolbox website.
New examples will be added over time and contributions are more than welcome. If you would like to add an example to this collection please email your MATLAB file to stefan.guettel@manchester.ac.uk. You can use any m-file of this collection as a template.
A simple illustration
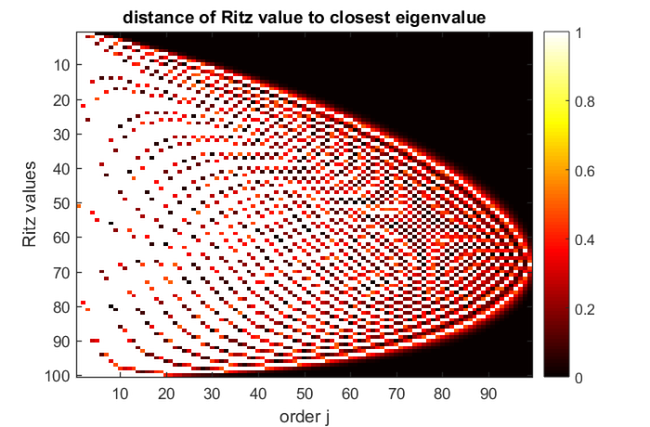
Here is a simple example illustrating the fascinating convergence behaviour of rational Ritz values [1]. The matrix 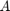 is diagonal with
is diagonal with 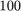 equispaced eigenvalues in the interval
equispaced eigenvalues in the interval ![$[1,100]$](index_eq07950079697856626477.png) . Using the rational Arnoldi method [3,4] implemented in rat_krylov, we compute Ritz values associated with rational Krylov spaces of increasing dimension with poles alternating between
. Using the rational Arnoldi method [3,4] implemented in rat_krylov, we compute Ritz values associated with rational Krylov spaces of increasing dimension with poles alternating between 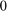 and
and  . We then visualize the distance of each Ritz value of order
. We then visualize the distance of each Ritz value of order 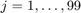 to its closest eigenvalue:
to its closest eigenvalue:
N = 100; m = 99; A = spdiags((1:m+1)', 0, N, N); b = ones(N, 1); xi = zeros(1, m); xi(1:2:end) = inf; [V, K, H] = rat_krylov(A, b, xi); Am = H(1:m, 1:m)/K(1:m, 1:m); R = ones(N, m); for j = 1:m ritz = eig(Am(1:j,1:j)); R(round(ritz),j) = abs(ritz - round(ritz)); end imagesc(R); colormap(hot(100)); colorbar xlabel('order j'); ylabel('Ritz values'); title('distance of Ritz value to closest eigenvalue')
Block rational Krylov methods
Ritz values can be slow to find repeated or tightly clustered eigenvalues. Block Krylov methods are often able to overcome this problem. Here we illustrate the difference between the Ritz value convergence in single-vector and block Krylov methods using the Wilkinson matrix [5], a symmetric tridiagonal matrix with pairs of nearly, but not exactly, equal eigenvalues. Using the block rational Arnoldi method [2], also implemented in rat_krylov, we now compute Ritz values associated with block polynomial Krylov spaces of block size  and
and  , respectively. We then pair off the Ritz values to their closest eigenvalues in descending order and visualize the distance between them using color.
, respectively. We then pair off the Ritz values to their closest eigenvalues in descending order and visualize the distance between them using color.
N = 100; m = 98; % m/s block Krylov iterations to perform W = wilkinson(N); evs = eig(W); for s = 1:2 % s is the block size rng(0), b = rand(N, s); xi = inf*ones(1, m/s); [~, K, H] = rat_krylov(W, b, xi); Am = H(1:m, 1:m)/K(1:m, 1:m); R = ones(N, m); for j = s:s:m ritz = sort(eig(Am(1:j,1:j)), 'descend'); evs_copy = evs; for i = 1:length(ritz) [y, ind] = min(abs(evs_copy - ritz(i))); evs_copy(ind) = inf; % pair Ritz val with unique ev R(ind, j-s+1:j) = y; end end figure(); imagesc(R); colormap(hot(100)); colorbar xlabel('order j'); ylabel('eigenvalue index'); title(['s = ', num2str(s), '']) end
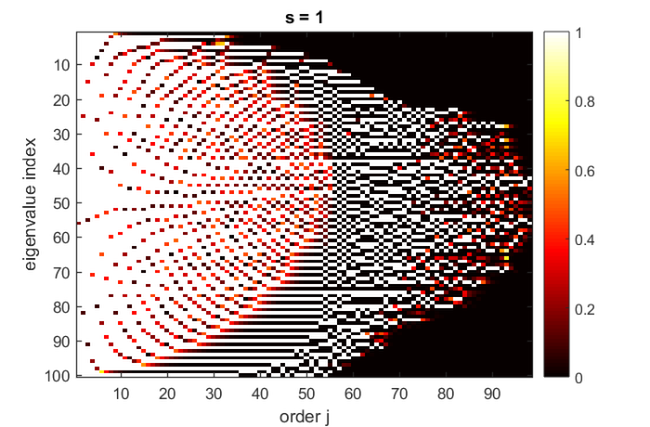
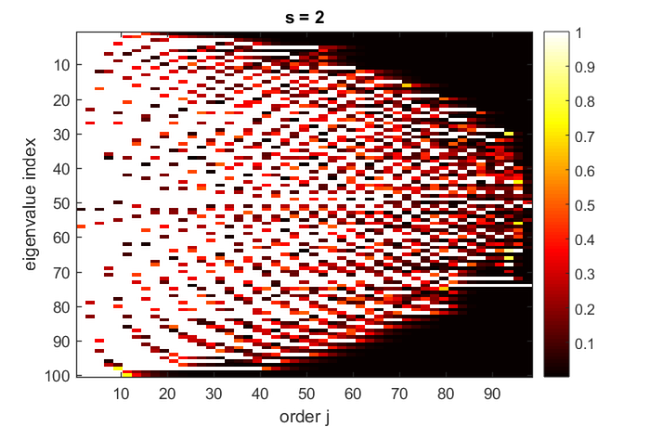
Most of the eigenvalues of the Wilkinson matrix appear in nearby pairs. The Ritz values computed with the single-vector Krylov method ( ) manage to approximate one of the eigenvalues in early iterations, but struggle to converge to the nearby second eigenvalue. In the block case (
) manage to approximate one of the eigenvalues in early iterations, but struggle to converge to the nearby second eigenvalue. In the block case ( ), pairs of eigenvalues are approximated more quickly.
), pairs of eigenvalues are approximated more quickly.
What else is in the RKToolbox?
In addition to Ruhe's (block) rational Krylov method with various advanced options (including user-defined inner products, exploitation of complex-conjugate shifts, orthogonalization, rerunning, and simulated parallelism), the RKToolbox currently contains
- algorithms for the implicit and explicit relocation of the poles of a rational Krylov space,
- a collection of utility functions and a gallery of special rational functions (e.g., Zolotarev approximants),
- an implementation of RKFIT, a robust algorithm for approximate rational least squares approximation, including automated degree reduction,
- the RKFUN class for numerical computations with rational functions, including support for MATLAB Variable Precision Arithmetic and the Advanpix Multiple Precision toolbox,
- the RKFUNM class, a matrix-valued generalization of RKFUNs, together with the ability to sample and solve nonlinear eigenvalue problems using the NLEIGS and AAA algorithms,
- the RKFUNB class for numerical computations with rational matrix-valued functions represented in block Krylov form, and
- the BARYFUN representation of rational functions in (generalized) barycentric form (with matrix-valued barycentric weights).
Please have a look at the other RKToolbox examples, which demonstrate some of these functionalities, and the guide. Happy RKToolbox-ing!
References
[1] B. Beckermann, S. Güttel, and R. Vandebril. On the convergence of rational Ritz values, SIAM J. Matrix Anal. Appl., 31(4):1740--1774, 2010.
[2] S. Elsworth and S. Güttel. The block rational Arnoldi method, SIAM J. Matrix Anal. Appl., 41(2):365--388, 2020.
[3] A. Ruhe. Rational Krylov: A practical algorithm for large sparse nonsymmetric matrix pencils, SIAM J. Sci. Comput., 19(5):1535--1551, 1998.
[4] A. Ruhe. The rational Krylov algorithm for nonsymmetric eigenvalue problems. III: Complex shifts for real matrices, BIT, 34(1):165--176, 1994.
[5] J. H. Wilkinson. The Algebraic Eigenvalue Problem, Oxford University Press, 1965.