The RKToolbox is a collection of scientific computing tools
based on rational Krylov techniques.
This plot visualizes the convergence of rational Ritz values for a symmetric matrix.
Hold on to see some slides with use cases of the RKToolbox.
based on rational Krylov techniques.
This plot visualizes the convergence of rational Ritz values for a symmetric matrix.
Hold on to see some slides with use cases of the RKToolbox.
Solve large-scale linear and nonlinear eigenvalue problems:
AB = util_linearise_nlep(A, Sigma, Xi, tol, Nmax); [V, K, H] = rat_krylov(AB, v, shifts);
Design rational filters using numerical arithmetic operations:
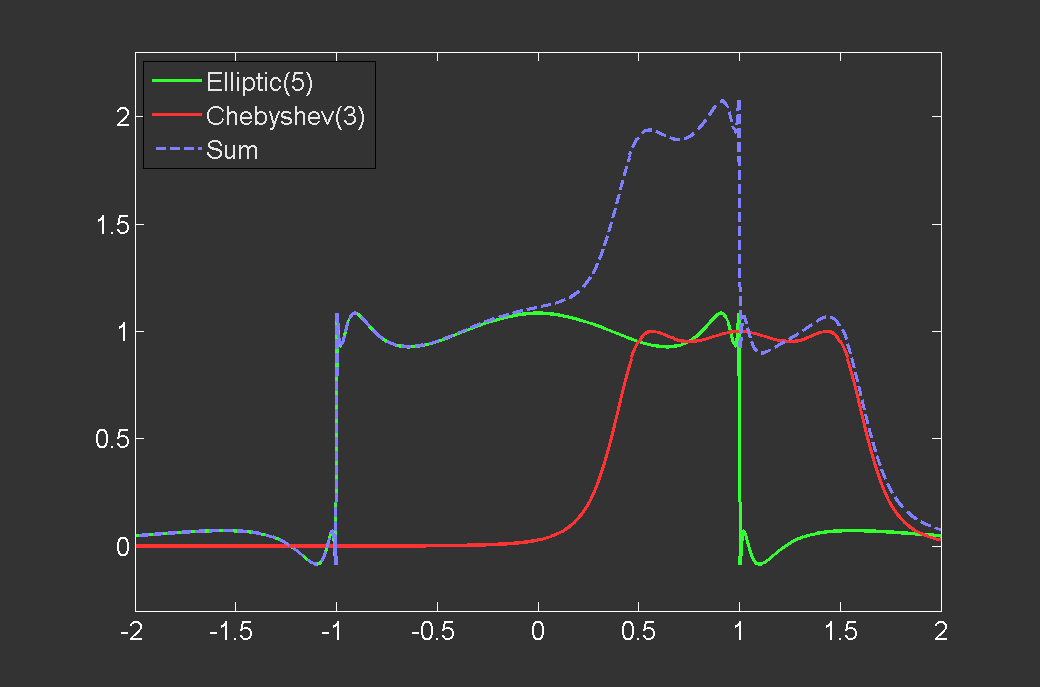
x = rkfun; f1 = rkfun('step',5); f2 = rkfun('cheby',3);
f2 = 1./(1 + 0.05*f2(2*x-2).^2); ezplot(f1+f2)
Partial fraction conversion and root-finding for rational functions:
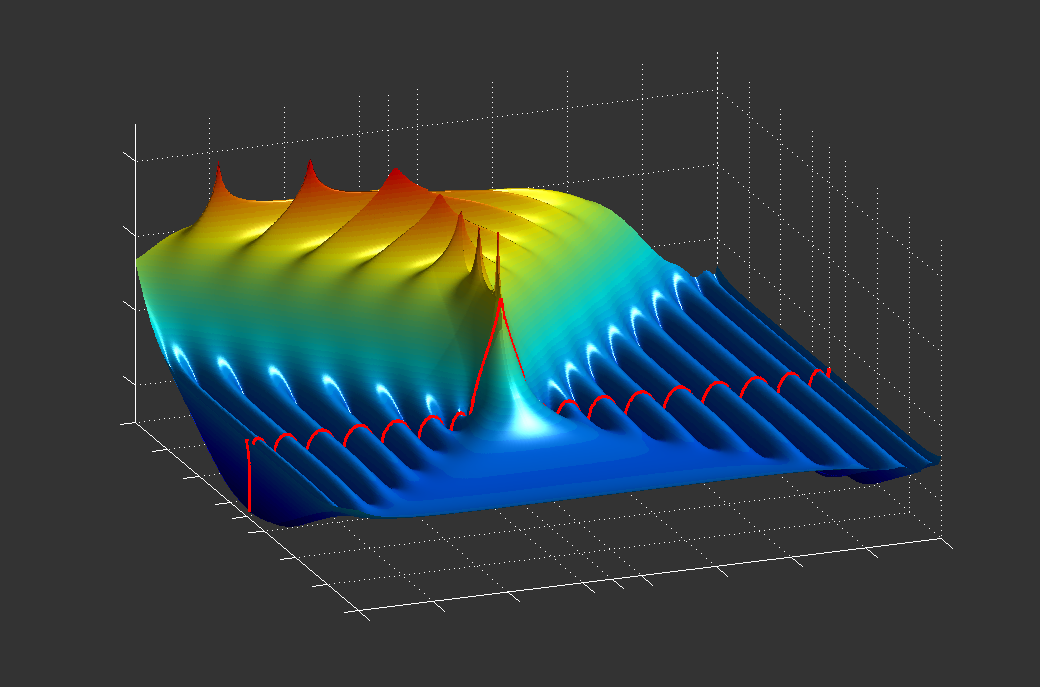
r = rkfun('(x^3 - x^2 + 1)/(x^4 + 1)'); s = rkfun('cayley');
res = residue(r(s)); rts = roots(r(s)); pls = poles(r(s));
Nonlinear fitting of transfer functions and pole identification:
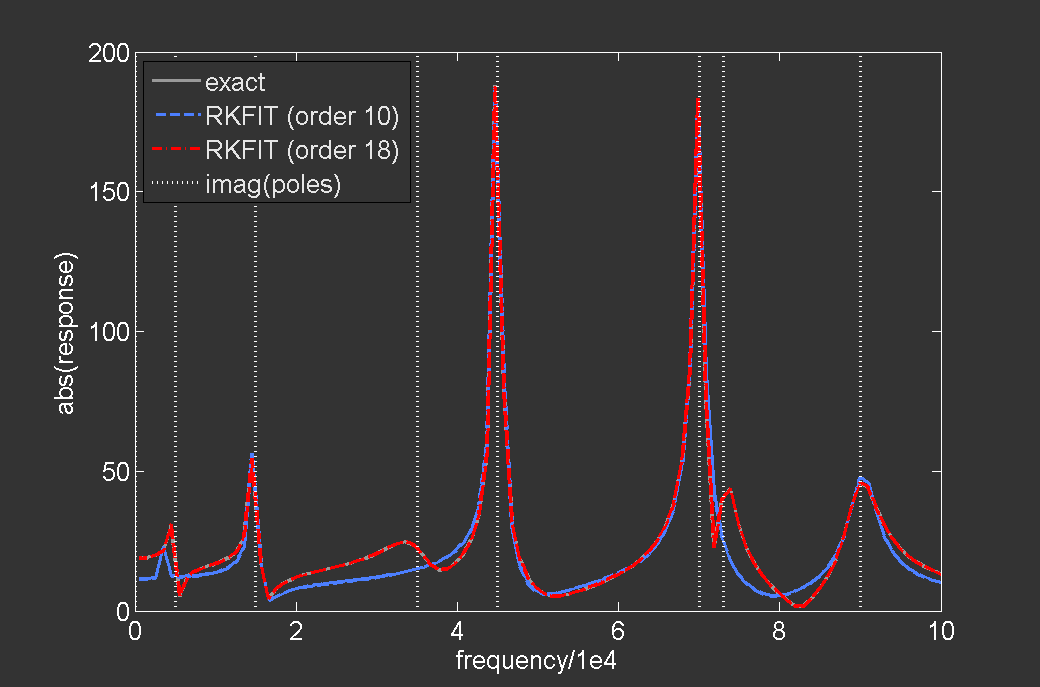
This slide shows the fitting of a frequency response using the RKFIT algorithm.
See this example for more details.
This slide shows the fitting of a frequency response using the RKFIT algorithm.
See this example for more details.
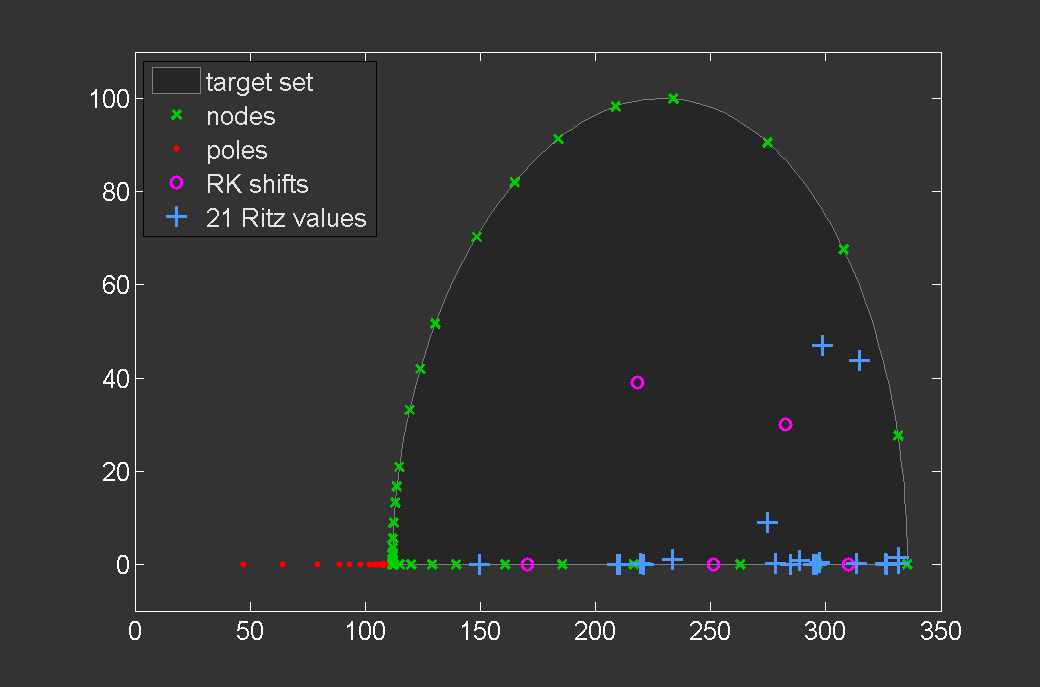
Parameter optimization for matrix function approximation:
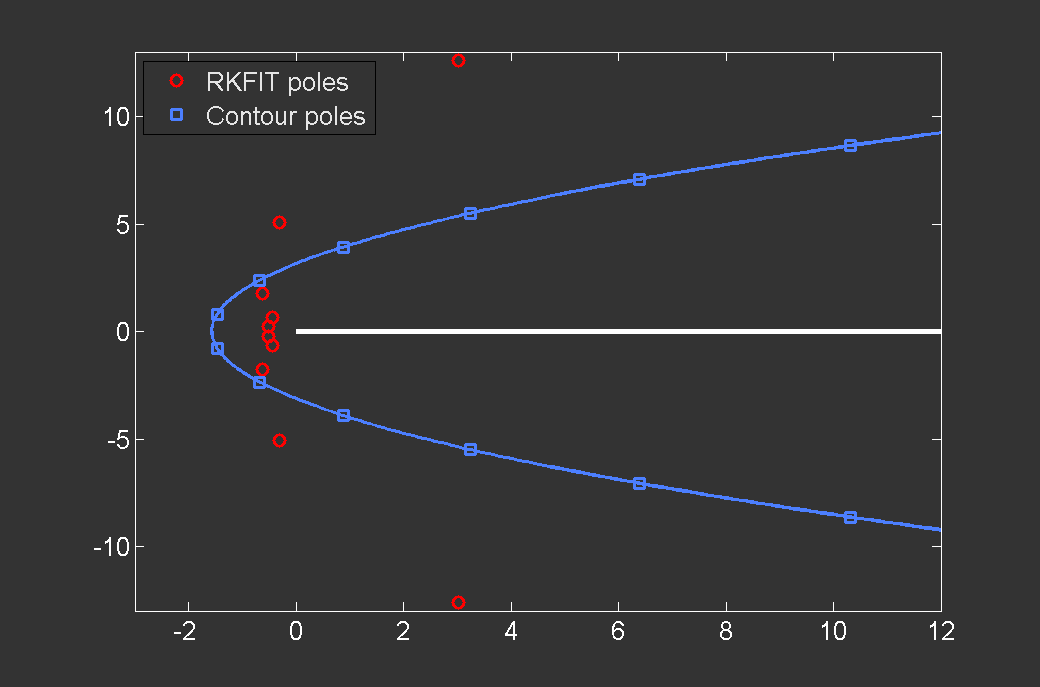
Optimized poles for the approximation of the matrix exponential function.
See this example for more details.
Optimized poles for the approximation of the matrix exponential function.
See this example for more details.
The RKToolbox is downloaded and installed within seconds:
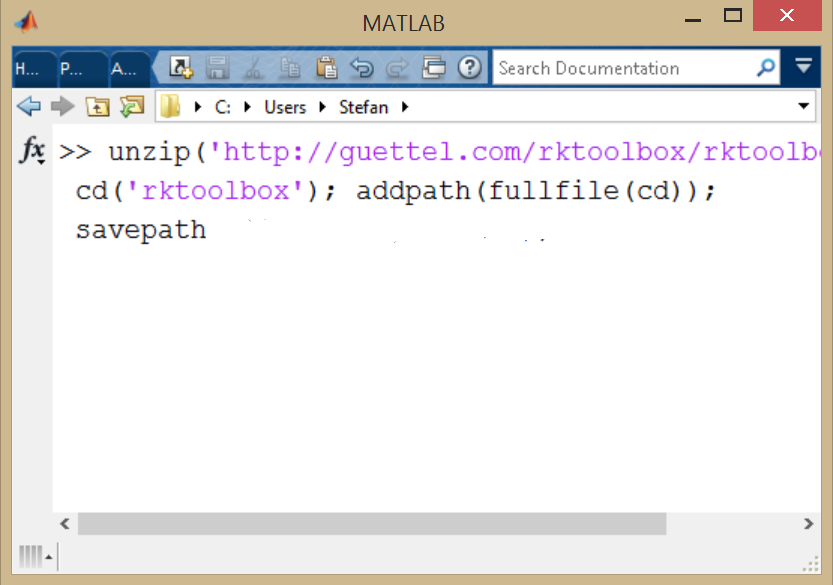
To get started, have a look at the guide and example collection.
Please contact us with any feedback or questions:
Mario Berljafa Steven Elsworth Stefan Güttel
