International Space Station model
Mario Berljafa and Stefan Güttel, June 2015Download PDF or m-file
Contents
Introduction
In this example we show how to use RKFIT [2, 3] from the RK Toolbox [1] to compute a lower-order model for the multiple-input/multiple-output dynamical system ISS 1R taken from [4]. We demonstrate the automated degree reduction capabilities of RKFIT, as well as its faster convergence compared to VFIT [5, 6, 7]. This example is explained in detail in [3, Section 6.1].
We now load the data and construct the matrices in real form as explained in [3, Section 3.5]. There are 3 input and 3 output channels, giving a total of 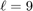 functions to fit. The frequencies we evaluate at are given in the vector w.
functions to fit. The frequencies we evaluate at are given in the vector w.
if exist('iss.mat') ~= 2 disp('File iss.mat not found. Can be downloaded from:') disp(['http://slicot.org/20-site/126-benchmark-examples' ... '-for-model-reduction']) return end load iss ell = 3*3; N = 2*length(w); F = zeros(N/2, ell); for j = 1:N/2 % We now evaluate the responses at 1i*w(j) from the state % space representation. The responses at -1i*w(j) is the % conjugated one. resp = full(C*((A-1i*w(j)*speye(length(A)))\B)); F(j, :) = resp(:).'; end Amat = util_build_real_matrix(1i*w); for j = 1:ell Fmat{j} = util_build_real_matrix(F(:, j)); end
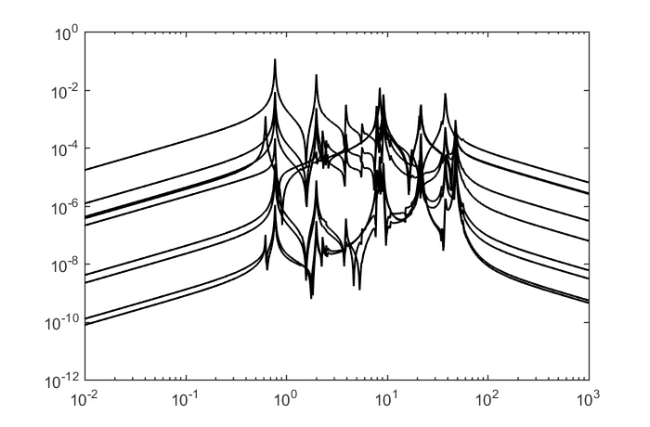
The following plot shows the magnitudes of the  transfer functions, over the frequency range w.
transfer functions, over the frequency range w.
figure for j = 1:ell loglog(w, abs(F(:, j)), 'k-'), hold on end
RKFIT and degree reduction
We search for approximants of type 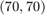 to reach a relative misfit below
to reach a relative misfit below 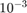 in at most
in at most 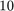 iterations. We use the real version, and impose no spectral weighting.
iterations. We use the real version, and impose no spectral weighting.
m = 70; tol = 1e-3; b = zeros(N, 1); b(1:2:end) = 1; init = util_ieee_poles(-2, 3, 1e-2, 70); [xi, ~, misfit, out] = rkfit(Fmat, Amat, b, init, ... struct('maxit', 10, ... 'tol', tol, ... 'real', 1, ... 'k', 0, ... 'safe', 1, ... 'stable', 0, ... 'reduction', 1));
The next plot shows the progress of the misfit during the iterations. For the first iteration (index 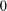 ) we show the misfit corresponding to the initial choice of poles.
) we show the misfit corresponding to the initial choice of poles.
figure iter = length(misfit); semilogy(0:iter, [out.misfit_initial misfit], 'ro-'), hold on semilogy([0 iter], [tol tol], 'k--') legend('RKFIT (70, 70)' , 'tolerance')
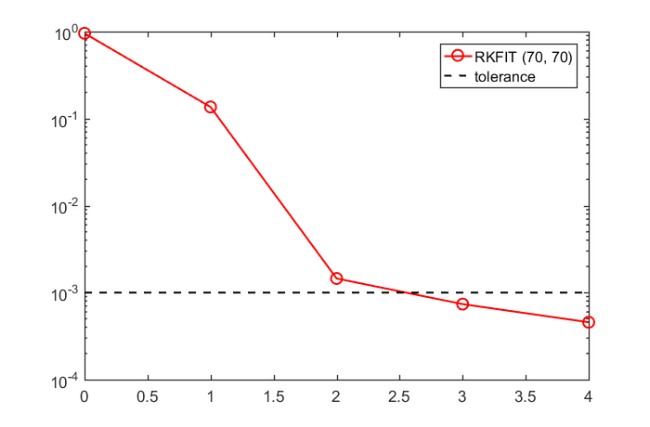
After the fourth iteration a reduction of  occurs. The misfit listed for iteration
occurs. The misfit listed for iteration 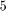 correspond to the misfit with the newly selected
correspond to the misfit with the newly selected 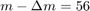 poles, as it is below the tolerance, no further RKFIT iterations are required. The
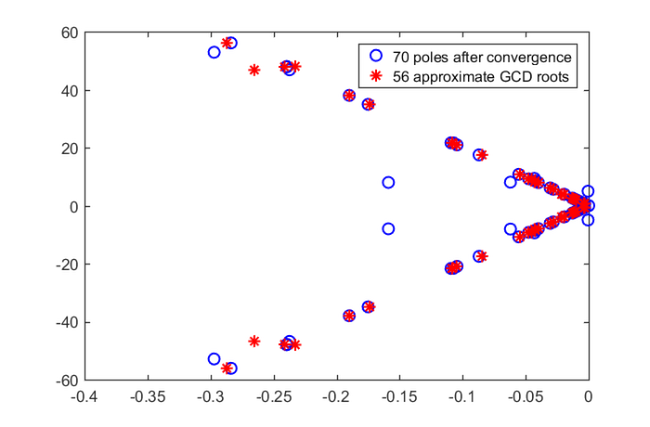
poles, as it is below the tolerance, no further RKFIT iterations are required. The 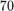 poles, and the
poles, and the 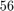 corresponding to the approximate GCD of the
corresponding to the approximate GCD of the 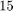 -dimensional nullspace are plotted in the next graph.
-dimensional nullspace are plotted in the next graph.
figure plot(real(out.xi_unreduced), imag(out.xi_unreduced), 'bo') hold on plot(real(out.xi_reduced), imag(out.xi_reduced), 'r*') legend('70 poles after convergence', '56 approximate GCD roots') axis([-.4,0,-60,60])
To demonstrate the benefit of the pole-selection process after the reduction we add a plot of the convergence of RKFIT with all initial 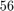 poles chosen without the acquired information, in a way similar to that of choosing the
poles chosen without the acquired information, in a way similar to that of choosing the 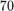 poles before.
poles before.
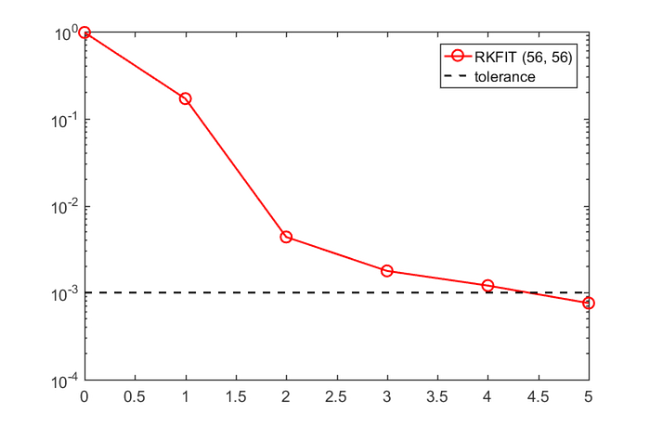
m = 56; init = util_ieee_poles(-2, 3, 1e-2, m); [xi, ~, misfit56, out56] = rkfit(Fmat, Amat, b, init, ... struct('maxit', 10, ... 'tol', tol, ... 'real', 1, ... 'k', 0, ... 'safe', 1, ... 'stable', 0, ... 'reduction', 0)); figure iter = length(misfit56); semilogy(0:iter, [out56.misfit_initial misfit56],'ro-'), hold on semilogy([0 iter],[tol tol], 'k--') legend('RKFIT (56, 56)' , 'tolerance')
Comparison with VFIT
We now compare RKFIT and VFIT. The vectfit3 implementation of VFIT is assumed to be available on MATLAB's search path.
if exist('vectfit3') ~= 2 disp('VFIT now available. Can be downloaded from:') disp('http://www.sintef.no/Projectweb/VECTFIT/Downloads/VFUT3/') return end
We use  again, and perform
again, and perform 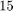 iterations with VFIT. Both VFIT with relaxed nontriviality constraint [6], and the original version with asymptotic nontriviality constraint [7] are tested. For the comparison we use two different sets of starting poles, and run RKFIT and the two versions of VFIT with them. The following plot shows the convergence results for both, with the iterations being stopped when the tolerance is reached.
iterations with VFIT. Both VFIT with relaxed nontriviality constraint [6], and the original version with asymptotic nontriviality constraint [7] are tested. For the comparison we use two different sets of starting poles, and run RKFIT and the two versions of VFIT with them. The following plot shows the convergence results for both, with the iterations being stopped when the tolerance is reached.
% Options for VFIT. opts_a.spy1 = 0; opts_a.spy2 = 0; opts_a.errplot = 0; opts_a.phaseplot = 0; opts_a.skip_pole = 0; opts_a.skip_res = 0; opts_a.cmplx_ss = 0; opts_a.legend = 0; opts_a.asymp = 2; opts_a.stable = 0; opts_a.relax = 0; opts_r = opts_a; opts_r.relax = 1; % Run tests for VFIT with the same poles as for RKFIT. xi = init; xi_r = init; for j = 1:15 [~, xi, ~, fit] = vectfit3(F.', 1i*w.', xi, ... ones(1, length(w)), opts_a); [~, xi_r, ~, fit_r] = vectfit3(F.', 1i*w.', xi_r, ... ones(1, length(w)), opts_r); vfit_a(j) = norm(fit-F.', 'fro')/norm(F, 'fro'); vfit_r(j) = norm(fit_r-F.', 'fro')/norm(F, 'fro'); end figure(5) len_a = min(find(vfit_a<1e-3)); len_r = min(find(vfit_r<1e-3)); semilogy(0:iter, [out56.misfit_initial misfit56], 'ro-'), hold on semilogy(1:len_a, vfit_a(1:len_a), 'bs-'), hold on semilogy(1:len_r, vfit_r(1:len_r), 'c^-'), hold on semilogy([0 100], [tol tol], 'k:') legend('RKFIT', 'VFIT', 'VFIT relaxed', 'tolerance') % Choose a new set of starting poles and repeat all three tests. rng(0) init = eig(rand(m)-10*eye(m)); [xi, ~, misfit56, out56] = rkfit(Fmat, Amat, b, init, ... struct('maxit', 10, ... 'tol', tol, ... 'real', 1, ... 'k', 0, ... 'safe', 1, ... 'stable', 0, ... 'reduction', 0)); xi = init; xi_r = init; for j = 1:15 [~, xi, ~, fit] = vectfit3(F.', 1i*w.', xi, ... ones(1, length(w)), opts_a); [~, xi_r, ~, fit_r] = vectfit3(F.', 1i*w.', xi_r, ... ones(1, length(w)), opts_r); vfit_a(j) = norm(fit-F.', 'fro')/norm(F, 'fro'); vfit_r(j) = norm(fit_r-F.', 'fro')/norm(F, 'fro'); end iter2 = length(misfit56); len_a2 = min(find(vfit_a<1e-3)); len_r2 = min(find(vfit_r<1e-3)); semilogy(1:len_a2, vfit_a(1:len_a2), 'bs--'), hold on semilogy(1:len_r2, vfit_r(1:len_r2), 'c^--'), hold on semilogy(0:iter2, [out56.misfit_initial misfit56], 'ro--'), hold on xlim([0 max([len_a, len_r, len_a2, len_r2])]), ylim([5e-4,2])
> In vectfit3 (line 423) In example_iss (line 162) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 44, tol = 1.119105e-13. > In vectfit3 (line 364) In example_iss (line 164) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 45, tol = 1.139089e-13. > In vectfit3 (line 423) In example_iss (line 162) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 55, tol = 1.119105e-13. > In vectfit3 (line 364) In example_iss (line 164) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 54, tol = 1.139089e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 14, tol = 1.119105e-13. > In vectfit3 (line 629) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 22, tol = 2.491340e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 15, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 22, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 20, tol = 1.119105e-13. > In vectfit3 (line 629) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 33, tol = 2.491340e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 21, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 33, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 30, tol = 1.119105e-13. > In vectfit3 (line 629) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 40, tol = 2.491340e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 31, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 38, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 36, tol = 1.119105e-13. > In vectfit3 (line 629) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 47, tol = 2.491340e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 37, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 47, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 45, tol = 1.119105e-13. > In vectfit3 (line 629) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 52, tol = 2.491340e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 45, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 51, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 49, tol = 1.119105e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 49, tol = 1.139089e-13. > In vectfit3 (line 629) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 56, tol = 2.491340e-13. > In vectfit3 (line 423) In example_iss (line 194) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 55, tol = 1.119105e-13. > In vectfit3 (line 364) In example_iss (line 196) In evalmxdom>instrumentAndRun (line 109) In evalmxdom (line 21) In publish (line 189) In x_examplepublish (line 96) Warning: Rank deficient, rank = 55, tol = 1.139089e-13.
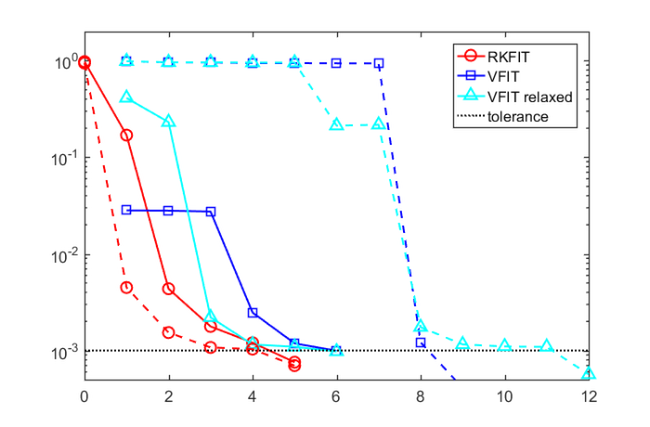
Note: The above warnings outputted by VFIT are due to ill-conditioned linear algebra problems being solved, a problem that is circumvented with RKFIT by the use of discrete-orthogonal rational basis functions.
References
[1] M. Berljafa and S. Güttel. A Rational Krylov Toolbox for MATLAB, MIMS EPrint 2014.56 (http://eprints.ma.man.ac.uk/2390/), Manchester Institute for Mathematical Sciences, The University of Manchester, UK, 2014.
[2] M. Berljafa and S. Güttel. Generalized rational Krylov decompositions with an application to rational approximation, SIAM J. Matrix Anal. Appl., 36(2):894--916, 2015.
[3] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[4] Y. Chahlaoui and P. Van Dooren. A collection of benchmark examples for model reduction of linear time invariant dynamical systems, MIMS EPrint 2008.22 (http://eprints.ma.man.ac.uk/1040/), Manchester Institute for Mathematical Sciences, The University of Manchester, UK, 2008.
[5] D. Deschrijver, M. Mrozowski, T. Dhaene, and D. De Zutter. Macromodeling of multiple systems using a fast implementation of the vector fitting method, IEEE Microw. Compon. Lett., 18(6):383--385, 2008.
[6] B. Gustavsen. Improving the pole relocating properties of vector fitting, IEEE Trans. Power Del., 21(3):1587--1592, 2006.
[7] B. Gustavsen and A. Semlyen. Rational approximation of frequency domain responses by vector fitting, IEEE Trans. Power Del., 14(3):1052--1061, 1999.