The FEAST algorithm for Hermitian eigenproblems
Mario Berljafa and Stefan GüttelDownload PDF or m-file
Contents
Introduction
FEAST is an algorithm for computing a few eigenpairs 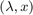 of a large sparse eigenvalue problem
of a large sparse eigenvalue problem 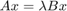 , where
, where  is a Hermitian
is a Hermitian 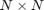 matrix, and
matrix, and 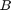 is Hermitian positive definite [4]. FEAST belongs to the class of contour-based eigensolvers which have recently attracted a lot of attention [3].
is Hermitian positive definite [4]. FEAST belongs to the class of contour-based eigensolvers which have recently attracted a lot of attention [3].
Mathematically, FEAST can be interpreted as a subspace iteration applied to a rational matrix function which serves the purpose of separating the wanted eigenvalues from the unwanted (i.e., it acts as a filter function). The RKFUN calculus of the RKToolbox is a convenient tool for working with rational functions and it allows for a simple implementation of the basic FEAST iteration. Of course, the full FEAST implementation comes with many more "bells and whistles," and in this tutorial we only aim to demonstrate the basic idea.
Model eigenvalue problem
Let us consider an eigenvalue problem 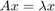 , where
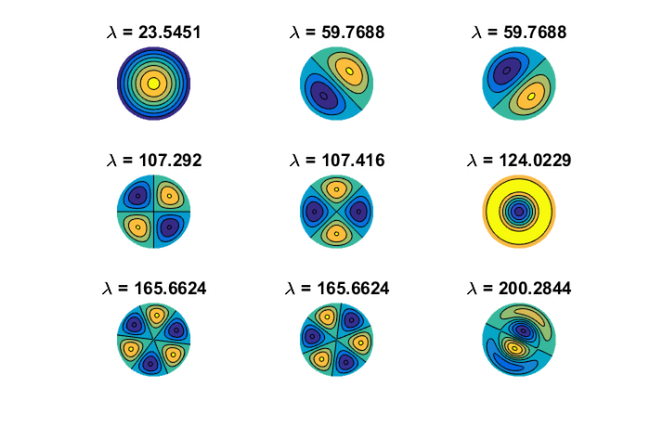
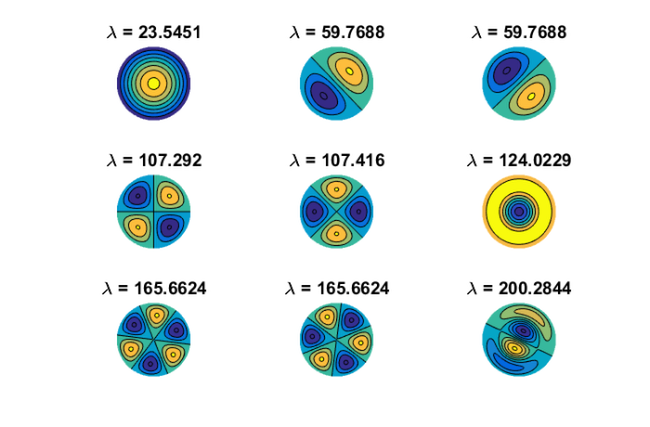
, where  is a finite-difference discretization of the Laplacian on a disk with homogeneous Dirichlet boundary conditions. Using MATLAB's eigs function, we first compute and visualize the
is a finite-difference discretization of the Laplacian on a disk with homogeneous Dirichlet boundary conditions. Using MATLAB's eigs function, we first compute and visualize the 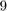 eigenvectors corresponding to the smallest eigenvalues of
eigenvectors corresponding to the smallest eigenvalues of  :
:
n = 150; G = numgrid('D', n); A = (n+1)^2*delsq(G); N = size(A, 1); B = speye(N); [V, D] = eigs(A, 9, 'SM'); [D, ind] = sort(diag(D)); V = V(:, ind); figure(1) for j = 1:9 subplot(3, 3, j) v = V(:, j); U = NaN*G; U(G>0) = full(v(G(G>0))); contourf(U); prism, axis square ij, axis off title(['\lambda = ' num2str(D(j))]); end
Constructing the filter function
Suppose we want to find these 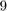 eigenmodes using FEAST, then we need to contruct a rational filter which would separate the corresponding eigenvalues of
eigenmodes using FEAST, then we need to contruct a rational filter which would separate the corresponding eigenvalues of  from the others. To this end, we combine a type
from the others. To this end, we combine a type 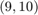 step function approximation for the interval
step function approximation for the interval ![$[-1,1]$](example_feast_eq01893875229900969577.png) with a linear transformation
with a linear transformation  mapping
mapping ![$[0,220]$](example_feast_eq15129795111818407232.png) to
to ![$[-1,1].$](example_feast_eq03030091630708792031.png) The result is a near-optimal rational filter
The result is a near-optimal rational filter  for the interval
for the interval ![$[0,220]$](example_feast_eq15129795111818407232.png) , attaining values very close to
, attaining values very close to  on that interval, and oscillating about
on that interval, and oscillating about 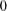 outside:
outside:
lmin = 0; lmax = 220; x = rkfun(); % independent variable x t = 2/(lmax-lmin)*x - (lmin+lmax)/(lmax-lmin); % map [lmin,lmax] -> [-1,1] s = rkfun('step', 5); r = s(t); figure, ezplot(r), hold on
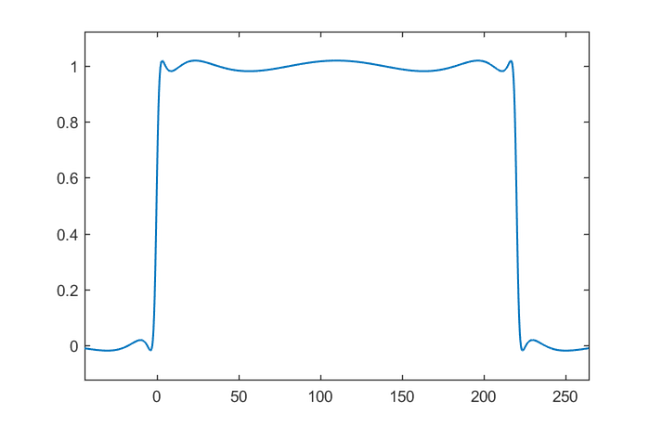
Let's compute the separation ratio between the approximate values for  and
and 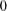 by finding the real local extrema of
by finding the real local extrema of  , and then finding the smallest/largest modulus of
, and then finding the smallest/largest modulus of  inside/outside
inside/outside ![$[0,220]$](example_feast_eq15129795111818407232.png) at these extrema. Such computations can become quite sensitive, in particular with rational functions of high degree. We therefore recommend performing this using the Advanpix Multipleprecision Toolbox [1]:
at these extrema. Such computations can become quite sensitive, in particular with rational functions of high degree. We therefore recommend performing this using the Advanpix Multipleprecision Toolbox [1]:
r = mp(r); extrema = roots(diff(r), 'real'); values = r(extrema); plot(extrema, values, 'ro') mini = min(abs(r(extrema(lmin < extrema & extrema < lmax)))); maxi = max(abs(r(extrema(lmin > extrema | extrema > lmax)))); plot([lmin, lmax], [mini, mini], 'k--') plot([-1e6, lmin], [maxi, maxi], 'k--') plot([lmax, 1e6], [maxi, maxi], 'k--')
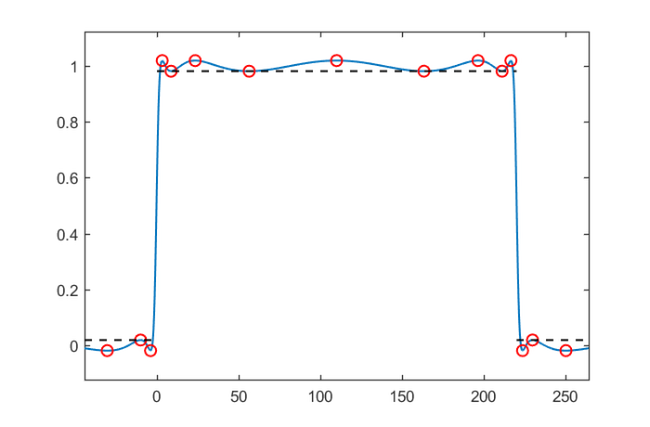
According to [2], the approximate convergence factor of FEAST for finding the eigenpairs in the interior of ![$[0,220]$](example_feast_eq15129795111818407232.png) is given by the following ratio:
is given by the following ratio:
ratio = double(maxi/mini)
ratio = 1.9351e-02
A simple FEAST implementation
We can easily verify this numerically by implementing a simple subspace iteration applied to  . Conveniently, the RKToolbox allows us to simply type
. Conveniently, the RKToolbox allows us to simply type  for computing
for computing  , the action of the rational filter on a basis
, the action of the rational filter on a basis  for the search space.
for the search space.
% Change to double precision. r = double(r); % Search space basis V of dimension m. m = 10; V = randn(N, m); for iter = 1:8 % Apply rational filter to V. V = r(A, V); % Compute and sort Ritz pairs. Am = V'*A*V; Bm = V'*B*V; [W, D] = eig(Am, Bm); [D, ind] = sort(diag(D)); W = W(:, ind); % B-normalize W. nrm = sqrt(diag(W'*Bm*W)); W = W/diag(nrm); % Form approximate eigenvectors. V = V*W; % Check residuals and number of eigenpairs inside % search iterval. Di = diag(D(lmin < D & D < lmax)); Vi = V(:, lmin < D & D < lmax); resid(iter) = norm(A*Vi - B*Vi*Di, 'fro'); nrvec(iter) = size(Vi, 2); end
Here is a plot of the residual norms after each FEAST iteration, together with the expected convergence factor, and the number of Ritz values inside the search iterval:
figure semilogy(resid, 'b-o'), hold on semilogy(1e10*ratio.^(1:iter), 'k--') for j = 1:iter hdl = text(j-.1,5*resid(j), num2str(nrvec(j))); set(hdl, 'FontSize', 14, 'Color', 'b') end xlim([.5, iter+.5]), xlabel('iteration') legend('residual norm','expected rate') ylim([1e-8, 1e6])
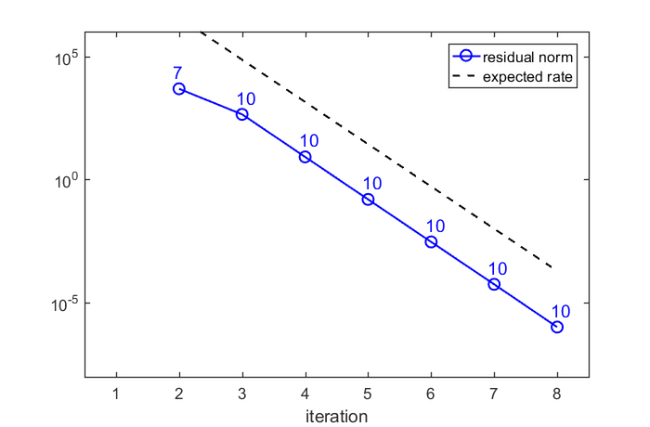
There is a very good agreement between the predicted and observed convergence. In the first iteration, no Ritz value is in the search interval, but after only 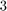 iterations we have found
iterations we have found 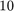 Ritz values. Indeed, looking at the 9th eigenvector in the plot above, we expect by symmetry that there will be a 10th eigenvalue corresponding to the same eigenvalue
Ritz values. Indeed, looking at the 9th eigenvector in the plot above, we expect by symmetry that there will be a 10th eigenvalue corresponding to the same eigenvalue  .
.
Remarks on parallel implementation
As mentioned above, our basic FEAST implementation is not at all efficient and serves only the purpose of a demonstration. A main feature of FEAST is its parallelism in evaluating 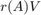 by using a partial fraction expansion of
by using a partial fraction expansion of  of the form
of the form
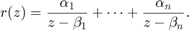
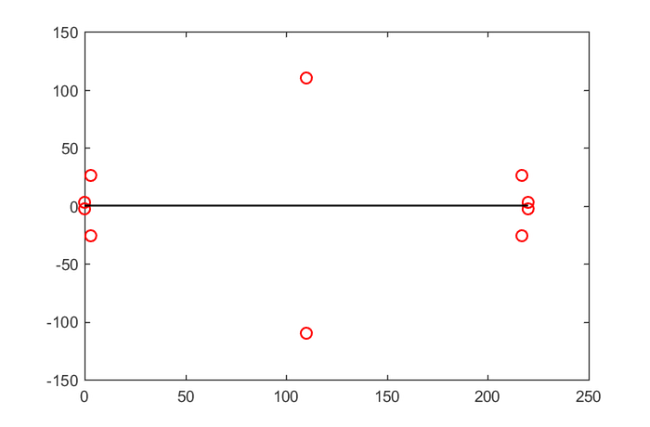
We can easily compute such an expansion using the residue command of the RKToolbox, again in multiple precision to avoid accuracy loss. Here is a plot of the poles of  in the complex plane, relative to the search interval
in the complex plane, relative to the search interval ![$[0,220]$](example_feast_eq15129795111818407232.png) :
:
[alpha,beta] = residue(mp(r)); figure plot(beta, 'ro'), hold on plot([lmin, lmax], [0, 0], 'k-')
That's it. The following command creates a thumbnail
figure(1), hold on, plot(NaN)
References
[1] Advanpix LLC., Multiprecision Computing Toolbox for MATLAB, ver 4.3.3.12213, Tokyo, Japan, 2017. http://www.advanpix.com/.
[2] S. Güttel, E. Polizzi, P. Tang, and G. Viaud. Zolotarev quadrature rules and load balancing for the FEAST eigensolver, SIAM J. Sci. Comput., 37(4):A2100--A2122, 2015.
[3] A. Imakura, L. Du, and T. Sakurai. A map of contour integral-based eigensolvers for solving generalized eigenvalue problems, http://arxiv.org/abs/1510.02572, 2015
[4] E. Polizzi. Density-matrix-based algorithm for solving eigenvalue problems, Phys. Rev. B, 79:115112, 2009.