Structure of rational Krylov projections
Mario Berljafa and Stefan Güttel, June 2015Download PDF or m-file
Contents
Introduction
Let 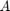 be a matrix of size
be a matrix of size 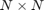 ,
, 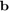 an
an 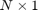 vector, and
vector, and  a positive integer. The polynomial Krylov space of order
a positive integer. The polynomial Krylov space of order 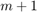 is defined as
is defined as 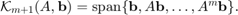 For simplicity we assume that
For simplicity we assume that 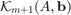 is of full dimension
is of full dimension 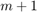 .
.
Let 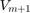 be an orthonormal matrix of size
be an orthonormal matrix of size 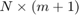 such that the leading
such that the leading  columns
columns 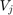 form a basis for
form a basis for 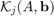 for
for  . It follows from the implicit Q theorem that the projection
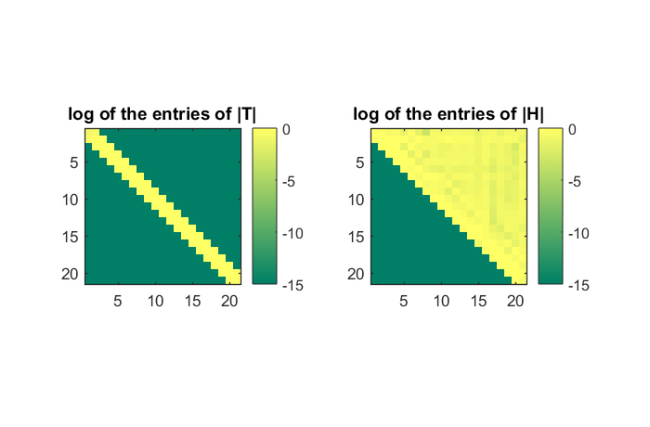
. It follows from the implicit Q theorem that the projection 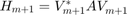 is an upper Hessenberg matrix; that is, all the elements below the first subdiagonal of
is an upper Hessenberg matrix; that is, all the elements below the first subdiagonal of 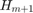 are zero. Moreover, if the matrix
are zero. Moreover, if the matrix 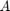 is symmetric so is the projection
is symmetric so is the projection  , and hence it is tridiagonal.
, and hence it is tridiagonal.
Below we visualize the aforementioned structure for a symmetric matrix (the plot on the left), and for a nonsymmetric matrix (the plot on the right).
N = 200; m = 20; % Polynomial Krylov space; infinite poles. xi = inf(1,m); % Symmetric matrix. A = gallery('tridiag', N); b = sum(eye(N, 15), 2); V = rat_krylov(A, b, xi); T = V'*A*V; % Nonsymmteric matrix. A = gallery('grcar', N); V = rat_krylov(A, b, xi); H = V'*A*V; figure(1), colormap('summer') subplot(121), imagesc(log10(abs(T))) colorbar, set(gca,'CLim',[-15,0]); axis square title('log of the entries of |T|') subplot(122), imagesc(log10(abs(H))) colorbar, set(gca,'CLim',[-15,0]); axis square title('log of the entries of |H|')
The aim of this note is to review the structure of the projection 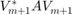 of
of 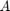 onto more general Krylov spaces; namely, rational Krylov spaces
onto more general Krylov spaces; namely, rational Krylov spaces 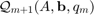 , which are defined in the next section. This structure has been studied, e.g., in [2, 4, 5, 8].
, which are defined in the next section. This structure has been studied, e.g., in [2, 4, 5, 8].
Rational Krylov space
Let 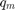 be a polynomial of degree at most
be a polynomial of degree at most  with roots disjoint from the spectrum of
with roots disjoint from the spectrum of 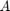 . The rational Krylov space
. The rational Krylov space  is defined as
is defined as  The roots of
The roots of 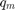 are called poles of the rational Krylov space. If
are called poles of the rational Krylov space. If 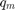 is a constant nonzero polynomial we recover the polynomial Krylov space.
is a constant nonzero polynomial we recover the polynomial Krylov space.
Semiseparable matrices
Let us look at the projection 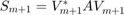 for a symmetric matrix
for a symmetric matrix 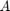 and
and 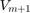 forming a basis for
forming a basis for  with
with 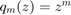 , i.e., a rational Krylov space with all poles equal to
, i.e., a rational Krylov space with all poles equal to 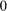 .
.
A = gallery('tridiag', N) + speye(N); xi = zeros(1,m); V = rat_krylov(A, b, xi); S = V'*A*V; figure(2), colormap('summer') imagesc(log10(abs(S))) colorbar, set(gca, 'CLim', [-15, 0]); axis square title('log of the entries of |S|')
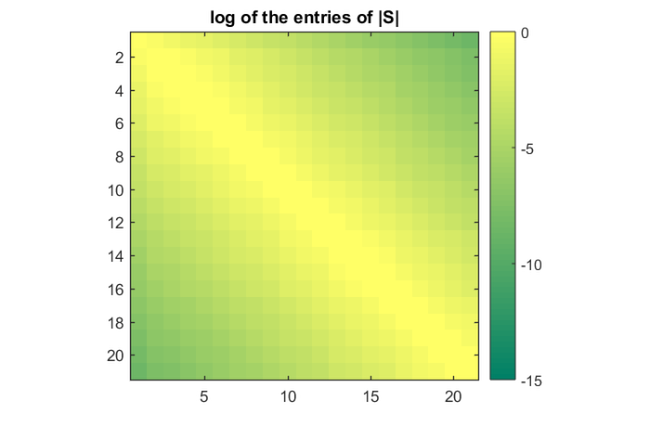
The projection is not tridiagonal, but it is semiseparable! A semiseparable matrix is one for which any submatrix consisting of elements in the strictly lower (upper, due to symmetry in this case) part is of rank at most  .
.
disp([rank(S(3:m, 1:2), 1e-15), ... rank(S(4:m, 1:3), 1e-15), ... rank(S(7:12, 1:4), 1e-15)])
1 1 1
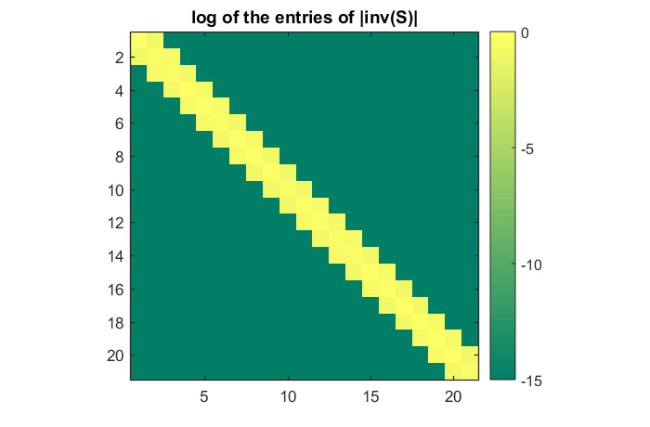
Note that 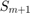 is nonsingular and its inverse is tridiagonal.
is nonsingular and its inverse is tridiagonal.
figure(3), colormap('summer') imagesc(log10(abs(S\eye(m+1)))) colorbar, set(gca, 'CLim', [-15, 0]); axis square title('log of the entries of |inv(S)|')
Semiseparable plus diagonal matrices
We now consider a more general rational Krylov space, having both finite and infinite poles. The ordering of the poles is irrelevant for the final space, but the structure of the projection may change depending on it.
Specifically, we look at a rational Krylov space with 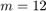 poles
poles 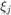 appearing in four groups. The first group consists of three poles at infinity, the second contains three finite poles, two infinite poles make the third group, and in the fourth there are four finite poles. The matrix
appearing in four groups. The first group consists of three poles at infinity, the second contains three finite poles, two infinite poles make the third group, and in the fourth there are four finite poles. The matrix 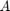 is chosen as nonsymmetric.
is chosen as nonsymmetric.
A = gallery('grcar', N); xi = [inf, inf, inf, ... -20, -10, 80, ... inf, inf, ... -20, 80, 80, -50];
The structure of 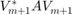 is related to the pole groups. Define the diagonal matrix of poles
is related to the pole groups. Define the diagonal matrix of poles 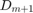 by setting
by setting 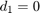 , and
, and 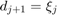 if
if  or
or 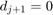 if
if 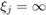 , for
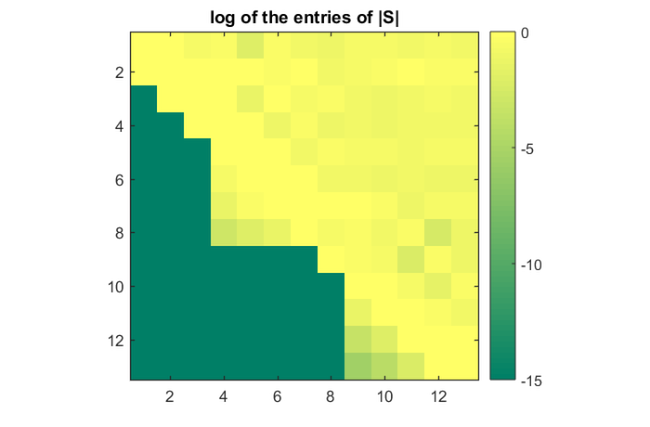
, for 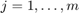 . Then the matrix
. Then the matrix  is semiseparable.
is semiseparable.
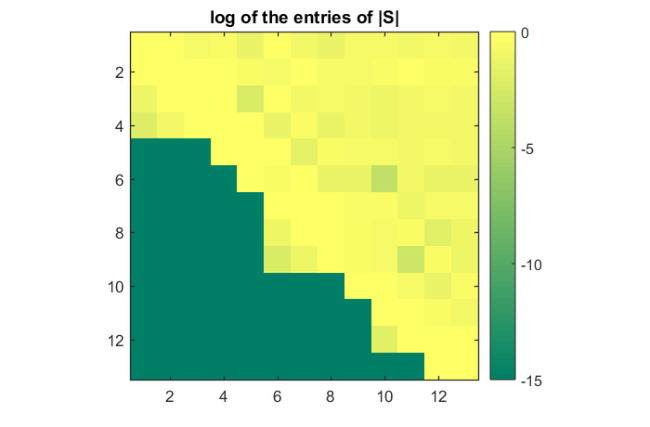
[V, K, H] = rat_krylov(A, b, xi); S = V'*A*V; D = diag([0 xi]); D(D == inf) = 0; S = S - D; figure(4), colormap('summer') imagesc(log10(abs(S))) colorbar, set(gca, 'CLim', [-15, 0]); axis square title('log of the entries of |S|')
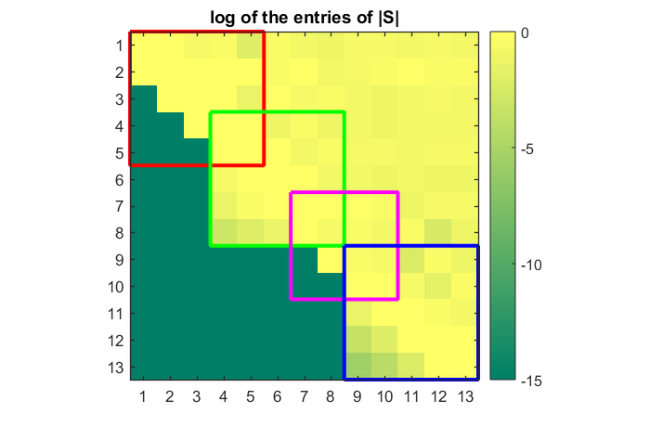
For each of the four pole groups there is a corresponding submatrix of 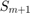 . The submatrices lie on the diagonal of
. The submatrices lie on the diagonal of 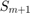 and share
and share  corner(s) with the neighbouring blocks. The two submatrices corresponding to the two groups with infinite poles are upper-Hessenberg, and the other two are inverse upper-Hessenberg.
corner(s) with the neighbouring blocks. The two submatrices corresponding to the two groups with infinite poles are upper-Hessenberg, and the other two are inverse upper-Hessenberg.
l1 = line([0, 0, 5, 5, 0]+.5, [0, 5, 5, 0, 0]+.5); l2 = line([3, 3, 8, 8, 3]+.5, [3, 8, 8, 3, 3]+.5); l3 = line([6, 6, 10, 10, 6]+.5, [6, 10, 10, 6, 6]+.5); l4 = line([8, 8, 13, 13, 8]+.5, [8, 13, 13, 8, 8]+.5); set([l1,l2,l3,l4],'LineWidth',3) set(l1,'Color','r'), set(l2,'Color','g') set(l3,'Color','m'), set(l4,'Color','b') set(gca, 'XTick', 1:13,'YTick',1:13)
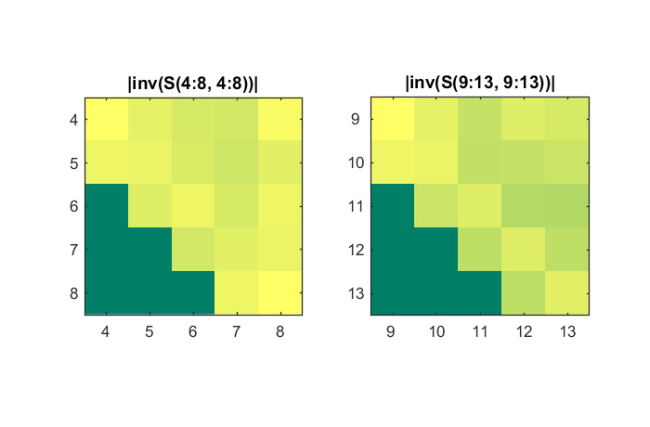
In the following plot we show the inverses of the second and fourth block, to confirm that they are indeed upper Hessenberg matrices.
figure(5), colormap('summer') subplot(121) imgsci = @(X, ii) imagesc(log10(abs(X(ii, ii)\eye(length(ii))))); imgsci(S, 4:8), set(gca,'CLim',[-15,0]); axis square set(gca,'XTick',1:5,'XTickLabel',4:8,'YTick',1:5,'YTickLabel',4:8) title('|inv(S(4:8, 4:8))|') subplot(122) imgsci(S, 9:13), set(gca,'CLim',[-15,0]); axis square set(gca,'XTick',1:5,'XTickLabel',9:13,'YTick',1:5,'YTickLabel',9:13) title('|inv(S(9:13, 9:13))|')
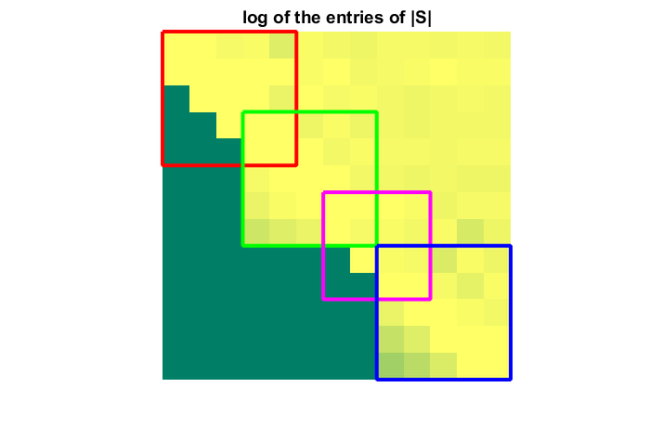
We now relocate the poles of the above rational Krylov space, as described in [1], and visualize the semiseparable structure. We take  groups of poles and can spot the corresponding overlapping upper-Hessenberg and inverse upper-Hessenberg blocks.
groups of poles and can spot the corresponding overlapping upper-Hessenberg and inverse upper-Hessenberg blocks.
xi_new = [-20, -30, ... inf, inf, inf, ... -30, -20, ... inf, inf, ... -30, ... inf, inf]; D_new = diag([0 xi_new]); D_new(D_new == inf) = 0; [~, ~, Q] = move_poles_expl(K, H, xi_new); S = Q*(S+D)*Q'-D_new; figure(6), colormap('summer') imagesc(log10(abs(S))), colorbar, set(gca, 'CLim', [-15, 0]); axis square, title('log of the entries of |S|')
The connection between rational Krylov spaces and semiseparable (plus diagonal) matrices has been used, for instance, for the development of short recurrences in rational quadrature rules, see e.g. [3, 6] and the references given therein. In [4, 5] the authors used it to approximate a rational Krylov space from a larger polynomial Krylov space. The examples shown here are for rather small matrices and low-dimensional rational Krylov spaces. For larger examples the semiseparable structure is often obscured by numerical roundoff and not reliably exploited, which is one of the reasons we prefer to work with the upper-Hessenberg representations for rational Krylov spaces, see e.g. [1, 7].
The following command is used to create a thumbnail.
figure(4), colorbar off, axis square, axis off
References
[1] M. Berljafa and S. Güttel. Generalized rational Krylov decompositions with an application to rational approximation, SIAM J. Matrix Anal. Appl., 36(2):894--916, 2015.
[2] D. Fasino. Rational Krylov matrices and QR steps on Hermitian diagonal-plus-semiseparable matrices, Numer. Linear Algebra Appl., 12(8):743--754, 2005.
[3] C. Jagels and L. Reichel. Recursion relations for the extended Krylov subspace method, Linear Algebra Appl., 434(7):1716--1732, 2011.
[4] T. Mach, M. Pranic, and R. Vandebril. Computing approximate extended Krylov subspaces without explicit inversion, Electron. Trans. Numer. Anal., 40:414--435, 2013.
[5] T. Mach, M. Pranic, and R. Vandebril. Computing approximate (block) rational Krylov subspaces without explicit inversion with extensions to symmetric matrices, Electron. Trans. Numer. Anal., 43:100--124, 2014.
[6] M. Pranic and L. Reichel. Rational Gauss quadrature, SIAM J. Numer. Anal., 52(2):832--851, 2014.
[7] A. Ruhe. Rational Krylov: A practical algorithm for large sparse nonsymmetric matrix pencils, SIAM J. Sci. Comput., 19(5):1535--1551, 1998.
[8] M. Van Barel, D. Fasino, L. Gemignani, and N. Mastronardi. Orthogonal rational functions and structured matrices, SIAM J. Matrix Anal. Appl., 26(3):810--829, 2005.