Compressing exterior Helmholtz problems
Stefan GüttelDownload PDF or m-file
Contents
Introduction
Finite difference (FD) methods are widely used for the numerical solution of partial differential equations. Due to their simplicity and potential for high computational efficiency they are often preferred to more sophisticated techniques like, e.g., finite element or spectral methods.
There is an intimite connection between FD grids, continued fractions, and rational apprpoximation, as is explained for example in [3, 4]. In particular [4] shows how to use the RKFIT method of this toolbox to 'compress' FD grids. By 'compressing an FD grid' we mean the task of computing an equivalent short-term recurrence FD grid with a small number of points that preserves essential features of the original grid. Problems like this arise, for example, when designing perfectly matched layers for the 2D variable-coefficient Helmholtz equation
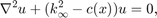
for ![$(x,y)\in [0,+\infty)\times [0,1]$](example_ehcompress_eq04480860712024501377.png) with a compactly supported offset function
with a compactly supported offset function 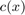 for the wavenumber
for the wavenumber 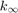 and appropriate boundary conditions. If the transverse differential operator
and appropriate boundary conditions. If the transverse differential operator 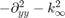 at
at 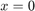 is discretized by a finite difference matrix
is discretized by a finite difference matrix 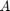 , then the above equation becomes a boundary value problem (BVP)
, then the above equation becomes a boundary value problem (BVP)
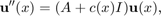
where the boundary conditions may be, for example, that  and
and  remains bounded for all
remains bounded for all 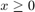 .
.
It is easy to verify that the Dirichlet-to-Neumann map at 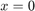 for the above BVP is a (possibly complicated) matrix function of
for the above BVP is a (possibly complicated) matrix function of 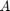 , i.e.,
, i.e., 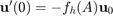 (using the notation of [4]). Since its version 2.5 the RKToolbox provides a utility function util_dtnfun for the (scalar) evaluation of
(using the notation of [4]). Since its version 2.5 the RKToolbox provides a utility function util_dtnfun for the (scalar) evaluation of 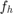 , corresponding to formula (2.3) in [4].
, corresponding to formula (2.3) in [4].
The main aim of [4] was to approximate 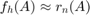 by a rational matrix function using RKFIT, and to convert the rational approximant
by a rational matrix function using RKFIT, and to convert the rational approximant 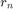 into continued fraction form. This continued fration form can then be interpreted as a finite difference approximation to the original BVP, giving rise to a perfectly matched layer for variable-coefficient Helmholtz equation on unbounded domains. We refer the reader to [4] for more details. The examples below reproduce the numerical experiments in that paper.
into continued fraction form. This continued fration form can then be interpreted as a finite difference approximation to the original BVP, giving rise to a perfectly matched layer for variable-coefficient Helmholtz equation on unbounded domains. We refer the reader to [4] for more details. The examples below reproduce the numerical experiments in that paper.
A two-layer waveguide example
This example reproduces the two-layer waveguide example in the introduction of [4]; see in particular Figure 1.2 therein. First, let us define the transversal operator 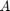 , which in this case is an indefinite Helmholtz operator with wavenumber
, which in this case is an indefinite Helmholtz operator with wavenumber 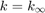 , and the number of grid points used along the waveguide.
, and the number of grid points used along the waveguide.
n = 151; k = 14; A = (n+1)^2*gallery('tridiag',n) - k^2*speye(n); L = 300; % length of waveguide in # grid points
Now we define the grid steps for the waveguide and replace the trailing grid steps by a Zolotarev PML [3]. (It is assumed that in the infinite layer we simply have the indefinite operator 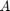 without further variation in wavenumber.)
without further variation in wavenumber.)
pml = 10; % # of PML points h = 1/(n+1)*ones(L+1,1); hh = h; % primal and dual grid steps e = eig(full(A)); % spectral subintervals for Zolotarev PML a1 = min(e(e<0)); b1 = max(e(e<0)); a2 = min(e(e>0)); b2 = max(e(e>0)); ratfun = mp(rkfun('invsqrt2h',a1,b1,a2,b2,pml,h(1))); [hp,hd,absterm,cnd,cf] = contfrac(ratfun); S = double([hp, hd]); % change to PML grid S(1,2) = S(1,2) + h(1)/2; hx = h; hxx = hh; hx(end+2-pml:end+1) = S(:,1); hxx(end+1-pml:end) = S(:,2); hxx(end+1) = NaN;
Now we specify the wavenumber in the  direction of the waveguide by defining the coefficient function
direction of the waveguide by defining the coefficient function 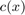 , which acts as an offset for the wavenumber. The total wavenumber is
, which acts as an offset for the wavenumber. The total wavenumber is  .
.
c = zeros(L,1);
c(1:150) = -9^2;
c0 = c(1);
c(end-pml:end) = 0; % in the infinite PML layer we assume c = 0
We build the complete matrix system.
T = spdiags([1./([hx(2:end);NaN].*[hxx(2:end);NaN]) , ... -1./(hx.*hxx)-1./([hx(2:end);NaN].*hxx)-[c;NaN;NaN] , ... 1./(hx.*[NaN;hxx(1:end-1)])],-1:1,L,L); M = kron(T,speye(n)) - kron(speye(L),A); u0 = zeros(n,1); u0(50) = 1/(n+1); rhs = [ -1/(hh(2)*hh(1))*u0 ; zeros((L-1)*n,1) ];
Solve and plot.
sol = M\rhs; Sol = [ u0, reshape(sol,n,L) ]; figure, hfig1 = pcolor(abs(Sol)); colormap pink, set(gca,'CLim',[0,7e-4]) set(hfig1,'LineStyle','none') axis ij, title('amplitude') hold on plot([150,150],[0,150],'--','Color',[1,1,1]) %plot([L-pml,L-pml],[0,150],'--','Color',[1,1,1]) set(gca,'XTick',1:50:L+1,'XTickLabel',0:50:L,'YTick',1:50:n+1,'YTickLabel',0:50:n)
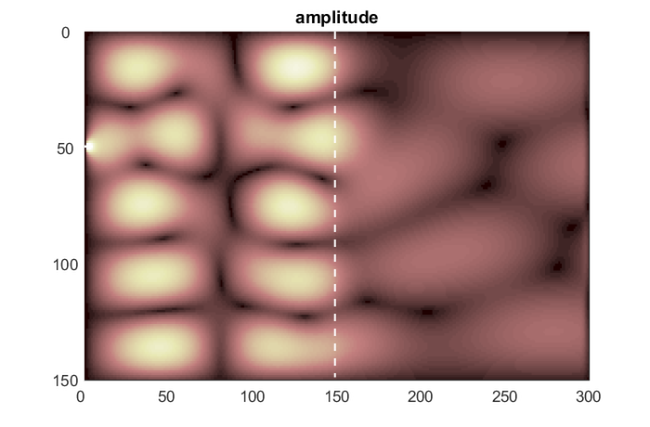
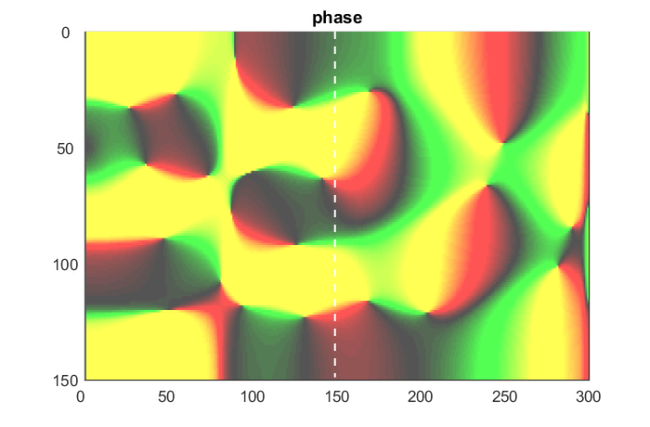
figure Ang = angle(Sol); Ang(Ang<0) = 2*pi+Ang(Ang<0); hfig2 = pcolor(Ang); set(hfig2,'LineStyle','none') axis ij, title('phase') set(gca,'CLim',[0,2*pi]) CC = util_colormapc(1,101); CC = CC + 0.33; CC(CC>1) = 1; colormap(CC); hold on, plot([150,150],[0,150],'--','Color',[1,1,1]) %plot([L-pml,L-pml],[0,150],'--','Color',[1,1,1]) set(gca,'XTick',1:50:L+1,'XTickLabel',0:50:L,'YTick',1:50:n+1,'YTickLabel',0:50:n)
Compute Neumann data from FD solution and compare with analytic solution:
b = hh(1)/2*(A + c0*speye(n))*u0 - (Sol(:,2)-u0)/h(1); [U,D] = eig(full(A)); F = U*diag(util_dtnfun(h(1),[ c(end:-1:1) ; c0],diag(D)))*U'; Fu0 = U*(util_dtnfun(h(1),[ c(end:-1:1) ; c0],diag(D)).*(U'*u0)); fprintf('Number of Zolotarev-PML points for the FD problem: %d\n', pml) fprintf('Accuracy of full FD solve w/ PML vs analytic DtN: %e', norm(b-Fu0))
Number of Zolotarev-PML points for the FD problem: 10 Accuracy of full FD solve w/ PML vs analytic DtN: 1.351368e-04
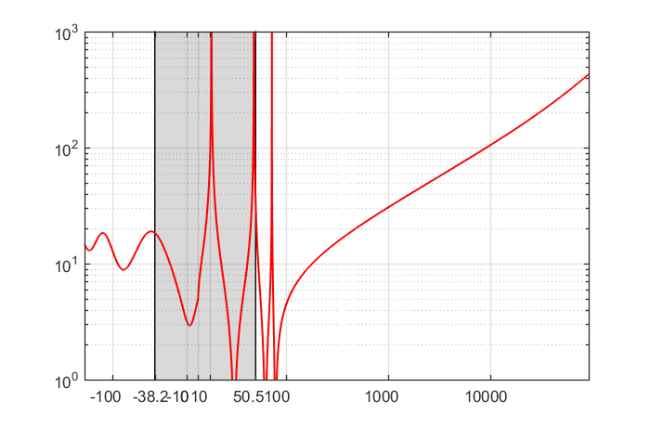
Now we plot the analytic DtN function over the spectral subintervals.
figure, hold off, semilogy(NaN), hold on lint = util_log2lin([b1,a2],[a1,b1,a2,b2],.2); fill([lint(1:2),lint([2,1])],[1e-25,1e-25,1e15,1e15],.85*[1,1,1],'LineStyle','-') ax = sort([ -10.^(5:-1:1) , b1 , 0 , a2, 10.^(1:5) ]); linax = util_log2lin(ax,[a1,b1,a2,b2],.2); set(gca,'XTick',linax,'XTickLabel',round(10*ax)/10) xlim([0,1]), ylim([1e-0,1e3]), grid on, set(gca,'layer','top') xx = sort([ -logspace(log10(-a1),log10(-b1),400) , linspace(b1,a2,450) , ... logspace(log10(a2),log10(b2),2001), e.' , 72.89 ]); xxt = util_log2lin(xx.',[a1,b1,a2,b2],.2).'; hh1 = semilogy(xxt,abs(util_dtnfun(h(1),[ c(end:-1:1) ; c0],xx)),'r-');
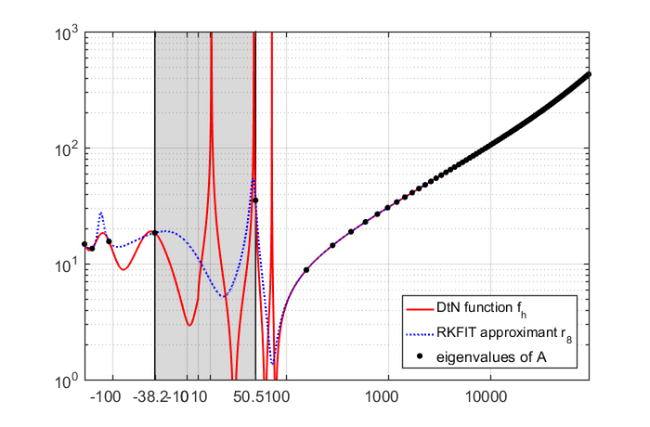
We now run RKFIT to approximate the DtN map.
param = struct; param.k = 1; % superdiagonal approximant param.tol = 0; % error tolerance param.reduction = 0; % turn off automatic degree reduction param.real = 0; % no exploitation of real arithmetic param.maxit = 30; % maximum number of rkfit iterations xi = inf*ones(1,7); % take m-1 initial poles [xi,ratfun,misfit,out] = rkfit(F,A,u0,xi,param); hh2 = semilogy(xxt,abs(ratfun(xx)),'b:'); % Plot eigenvalues on top et = util_log2lin(e.',[a1,b1,a2,b2],.2).'; hh3 = semilogy(et,abs(util_dtnfun(h(1),[c(end:-1:1); c0],e)),'k.','MarkerSize',16); legend([hh1,hh2,hh3],'DtN function f_h','RKFIT approximant r_8', ... 'eigenvalues of A','Location','SouthEast');
Other examples
The other examples in [4] can be reproduced with the following scripts:
Example 6.1 - constant coefficient and 1D indefinite Laplacian
Example 6.2 - constant coefficient and 2D indefinite Laplacian
Example 6.3 - uniform approximation on indefinite interval
Example 7.1 - truly variable-coefficient case with 2D indefinite Laplacian
References
[1] Advanpix LLC., Multiprecision Computing Toolbox for MATLAB, ver 3.9.4.10481, Tokyo, Japan, 2016. http://www.advanpix.com/.
[2] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[3] V. Druskin, S. Güttel, and L. Knizhnerman. Near-optimal perfectly matched layers for indefinite Helmholtz problems, SIAM Rev., 58(1):90--116, 2016.
[4] V. Druskin, S. Güttel, and L. Knizhnerman. Compressing variable-coefficient exterior Helmholtz problems via RKFIT, MIMS EPrint 2016.53 (http://eprints.ma.man.ac.uk/2511/), Manchester Institute for Mathematical Sciences, The University of Manchester, UK, 2016.