The block AAA algorithm

Ion Victor Gosea and Stefan Güttel, July 2020Download PDF or m-file

Contents

Introduction

Since version 2.9 the RKToolbox provides two new utility functions util_block_aaa and util_rmse for working with rational functions represented in a generalized barycentric form with matrix-valued weights,

$R(z) = \left(\displaystyle \sum_{i=0}^d W_i/(z-z_i)\right)^{-1} \left(\displaystyle \sum_{i=0}^d W_i F(z_i)/(z-z_i)\right).$

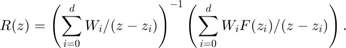
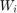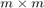In this notation, the $W_i$ are $m\times m$ nonsingular weight matrices, the 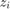$z_i$ are pairwise distinct barycentric support points in the complex plane, and the 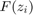$F(z_i)$ are $m\times n$ matrices. Different from the representation of rational functions computed by the RKFIT method [1], the AAA method [5] and its surrogate [2] and set-valued variants [4], the rational function 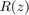$R(z)$ has a nonscalar "denominator matrix polynomial." See [3] for more details and a number of numerical experiments with different representations of rational matrix-valued functions.

Demonstration

We focus on a simple 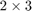$2\times 3$ matrix-valued function $F(z)$ to demonstrate the use of util_block_aaa. This function is defined as below and we sample it at 20 equidistant points on the interval $[0,10]$:

F = @(z) [ 1/(z+1)      1/(z^2-5)             z ;
           1/(z^2+5+1i) (2+z^2)/(z^3+3*z^2+1) 7 ];
pts = linspace(0,10,20);

Together with an error tolerance tol and a number of maximal iterations maxit, we have all that is needed to reapproximate 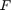$F$ using util_block_aaa:

opts.tol = 1e-12;
opts.maxit = 10;
[R,rmse,out] = util_block_aaa(F,pts,opts);

The output R is a baryfun object and we can display its info as follows:

disp(R)

	BARYFUN object of block size 2-by-3 and degree 5.

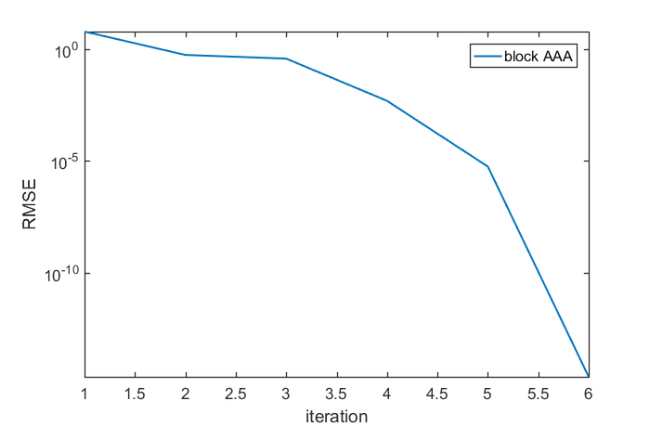
The output rmse stores the root mean squared error over all sampling points for each iteration of the block AAA method. In this case, we have resolved 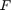$F$ to about machine precision after 6 iterations:

semilogy(rmse)
axis tight, hold on
legend('block AAA')
xlabel('iteration'), ylabel('RMSE')
disp(['The final RMSE is ' num2str(util_rmse(pts,F,R)) ])

The final RMSE is 2.3012e-15

References

[1] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.

[2] S. Elsworth and S. Güttel. Conversions between barycentric, RKFUN, and Newton representations of rational interpolants, Linear Algebra Appl., 576:246--257, 2019.

[3] I. V. Gosea and S. Güttel. Algorithms for the rational approximation of matrix-valued functions, arXiv preprint 2003.06410v1, 2020. (https://arxiv.org/abs/2003.06410)

[4] P. Lietaert, J. Perez, B. Vandereycken, and K. Meerbergen. Automatic rational approximation and linearization of nonlinear eigenvalue problems, arXiv preprint 1801.08622, 2018. (https://arxiv.org/pdf/1801.08622.pdf)

[5] Y. Nakatsukasa, O. Sete, and L. N. Trefethen. The AAA algorithm for rational approximation, SIAM J. Sci. Comput., 40(3):A1494--A1522, 2018.

Published with MATLAB® R2016a