The third and fourth Zolotarev problems
Alex Townsend, October 2016Download PDF or m-file
Contents
Introduction
In 1877, Yegor Ivanovich Zolotarev wrote an article that poses and solves four problems [5]: the first two are about polynomial approximation, while the third and fourth are about rational functions. These problems have become known as Zolotarev's first, second, third, and fourth problems. In this example we focus on Zolotarev's third and fourth problems. Recently, these problems have become important in numerical linear algebra because of a recursive construction of spectral projectors of matrices [3, 4].
Zolotarev's fourth problem
We start with the Zolotarev's fourth problem as it is perhaps easier than the third problem to visualize. Given two disjoint closed complex sets  and
and 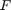 , Zolotarev's fourth problem is to find the rational function
, Zolotarev's fourth problem is to find the rational function  , where
, where 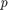 and
and 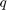 are polynomials of degree
are polynomials of degree 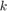 , that deviates least from the sign function on
, that deviates least from the sign function on 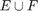 , i.e.,
, i.e.,
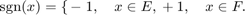
For general sets  and
and 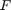 , the solution to Zolotarev's fourth problem is not known explicitly; however, there are a handful of special cases where the rational function can be given in closed form. The most important special case is when
, the solution to Zolotarev's fourth problem is not known explicitly; however, there are a handful of special cases where the rational function can be given in closed form. The most important special case is when  and
and 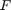 are real disjoint intervals.
are real disjoint intervals.
For example, if ![$E = [-b,-1]$](example_zolotarev_eq05184243193873580565.png) and
and ![$F = [1,b]$](example_zolotarev_eq01389434467423910546.png) with
with 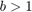 then an explicit solution to Zolotarev's fourth problem is known. It is implemented in RKToolbox's rkfun.gallery command. Here, we plot the extremal rational function
then an explicit solution to Zolotarev's fourth problem is known. It is implemented in RKToolbox's rkfun.gallery command. Here, we plot the extremal rational function 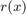 for degree
for degree 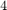 (
(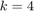 ) and also superimpose on the plot the approximation error:
) and also superimpose on the plot the approximation error:
b = 3; % E = [-b,-1] and F = [1,b] k = 4; % Degree of rational approximant to sign. r = rkfun.gallery('sign', k/2, b); % Solution to Z's fourth problem % Plot the computed rational function: x = linspace(-5, 5, 1000); y1 = linspace(-3, -1, 1000); y2 = linspace(1, 3, 1000); fill([-b -1 -1 -b -b], 1.5*[-1 -1 1 1 -1], .9*[1 1 1] ), hold on fill([b 1 1 b b], 1.5*[-1 -1 1 1 -1], .9*[1 1 1] ) [~,l1,l2] = plotyy(x, r(x), [y1 0 y2], [(1-abs(r(y1))) NaN (1-abs(r(y2)))]); l1.LineWidth = 2; l2.LineWidth = 2; text(-2.1,-1.4,'E','fontsize',16) text(2,-1.4,'F','fontsize',16) title('best R_{44} approximant to sign') xlabel('x'), hold off
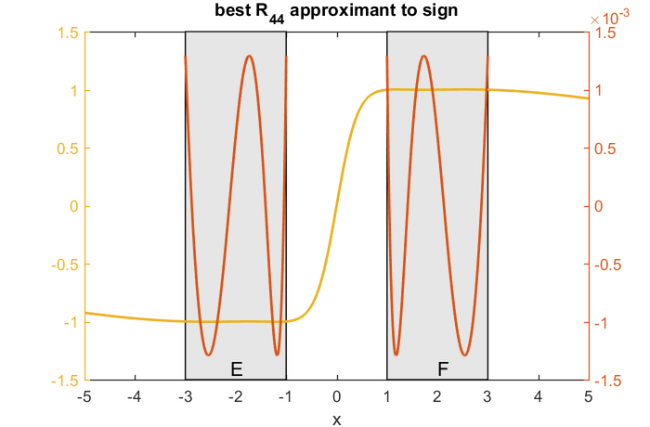
The explicit solution of Zolotarev's fourth problem involves Jacobi elliptic functions and complete elliptic integrals. We will not give its formula here, but it can be found scattered throughout the literature (see [1, Sec. 51, Tab. 2, No. 7 & 8]). The MATLAB code in rkfun.gallery uses this explicit formula.
You will notice that the error 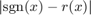 equioscillates precisely
equioscillates precisely  times on both
times on both ![$[-b,-1]$](example_zolotarev_eq02716342880001962606.png) and
and ![$[1,b]$](example_zolotarev_eq10763439698486525537.png) . This verifies the optimality of
. This verifies the optimality of 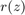 [1, Sec. 51]. Since the error equioscillates between a value of
[1, Sec. 51]. Since the error equioscillates between a value of 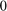 and
and  , there is a number
, there is a number 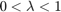 such that
such that
![$$\sup_{x\in [-b,-1]\cup [1,b]} | x - {\rm sgn}(x) | = \frac{1-\lambda}{1+\lambda}.$$](example_zolotarev_eq10708357565115181479.png)
The value for 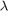 is known to satisfy the equation
is known to satisfy the equation 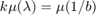 [1, Sec. 51], where
[1, Sec. 51], where 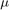 is the so-called Groetzsch ring function. The Groetzsch ring function
is the so-called Groetzsch ring function. The Groetzsch ring function ![$\mu:[0,1]\rightarrow[0,\infty)$](example_zolotarev_eq07561095297023396750.png) is defined as the ratio of the complete elliptic integral and its complement. It looks like this:
is defined as the ratio of the complete elliptic integral and its complement. It looks like this:
mu = @(lam) pi/2*ellipk( sqrt(1-lam.^2) )./ellipk( lam ); lam = linspace(0, 1, 10000); vals = zeros(numel(lam), 1); for j = 1:numel(lam), vals(j) = mu(lam(j)); end plot(lam, vals, 'linewidth',2), xlabel('\lambda') title('Groetzsch ring function'), hold off
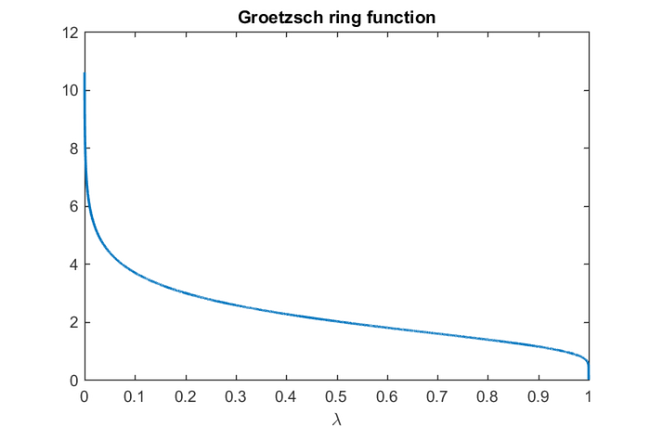
Since 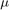 is a monotonically decreasing function, there is a unique
is a monotonically decreasing function, there is a unique 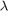 that solves
that solves 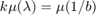 . We can find it via bisection:
. We can find it via bisection:
lam1 = 0; lam2 = 1; lam_opt = .5; target = mu(1/b)/k; for step = 1:50 % 50 steps finds the root to 16-digits. lam_opt = mean( [lam1 lam2] ); mid = mu( lam_opt ) - target; lam1 = lam1 + (mid>0).*(lam_opt - lam1); lam2 = lam2 + (mid<=0).*(lam_opt - lam2); end
We can verify that this is the correct 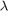 by comparing it to the observed error computed by RKToolbox:
by comparing it to the observed error computed by RKToolbox:
format longe
E4_error_lambda = (1-lam_opt)/(1+lam_opt)
E4_error_observed = max(1-abs(r(y1)))
E4_error_lambda =
1.292026239994933e-03
E4_error_observed =
1.292026239994693e-03
How well do rational functions approximate the sign function?
Zolotarev's fourth problem shows us that rational functions converge geometrically with respect to the degree 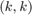 to the
to the 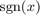 function defined on real disjoint intervals. In particular, from these explicit expressions it is known that [2, eqn. (A.5)]
function defined on real disjoint intervals. In particular, from these explicit expressions it is known that [2, eqn. (A.5)]
![$$ \sup_{x\in [-b,-1]\cup [1,b]} | r(x) - {\rm sgn}(x) | \leq 4e^{-k\frac{\pi^2}{2\mu(1/b)}}, $$](example_zolotarev_eq01734903719766060432.png)
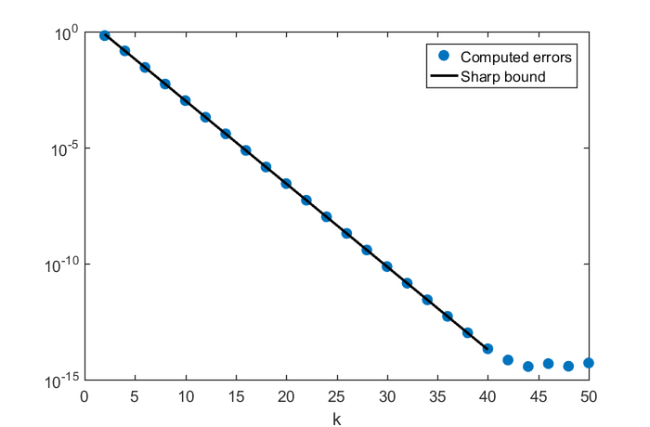
which is asymptotically a sharp upper bound. Here, is the computed approximation error ![$\sup_{x\in [-b,-1]\cup [1,b]}| r(x) - {\rm sgn}(x) |$](example_zolotarev_eq07668890174777406248.png) and the upper bound above when
and the upper bound above when 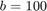 .
.
b = 100; % E = [-b,-1] and F = [1,b] y = linspace(-b, -1, 1000); for k = 2:2:50 r = rkfun.gallery('sign', k/2, b); % Solution to Z's fourth problem r_error(k/2) = max(abs(r(y)+1)); end semilogy(2:2:50, r_error,'.', 'markersize', 30), hold on semilogy(2:2:40, 4*(exp(pi^2/2/mu(1/b))).^(-(2:2:40)), 'k-', 'linewidth',2) legend('Computed errors', 'Sharp bound') xlabel('k'), hold off hold off
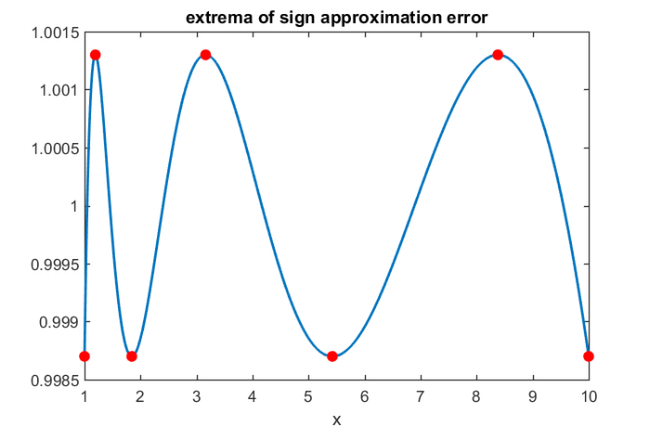
The location of the extrema of the error 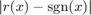 on
on ![$[-b,-1]$](example_zolotarev_eq02716342880001962606.png) and
and ![$[1,b]$](example_zolotarev_eq10763439698486525537.png) are also known explicitly. They are related to the Jacobi elliptic functions. Here, we demonstrate this when
are also known explicitly. They are related to the Jacobi elliptic functions. Here, we demonstrate this when 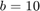 .
.
k = 6; % rational degree b = 10; % sign function on [-10,-1]\cup [1,10] r = rkfun.gallery('sign', k/2, b); % Extrema for [-1,-1/b]\cup [1/b,1]: K = ellipke(1-1/b^2); [sn, cn, dn] = ellipj((0:k)*K/k, 1-1/b^2); extrema = b*dn; % Transplant to [-b,-1]\cup [1,b] x = linspace(1, b, 1000); plot(x, r(x), 'linewidth', 2), hold on, plot(extrema, r(extrema), '.r', 'markersize', 30) title('extrema of sign approximation error') xlabel('x'), hold off
Zolotarev's third problem
Zolotarev's third problem is also related to rational approximation, but this time the problem is to find a rational function that is as small as possible on a set  while being
while being 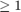 in absolute value on another set
in absolute value on another set 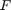 . More formally, given two disjoint closed complex sets
. More formally, given two disjoint closed complex sets  and
and 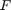 , Zolotarev's third problem is to find the rational function
, Zolotarev's third problem is to find the rational function  , where
, where 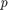 and
and 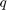 polynomials of degree
polynomials of degree 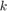 , such that
, such that 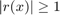 for
for 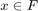 while
while 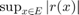 is as small as possible. Therefore,
is as small as possible. Therefore, 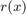 is the extremal rational function that attains the following infimum:
is the extremal rational function that attains the following infimum:
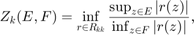
where 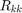 denotes the space of rational functions of degree at most
denotes the space of rational functions of degree at most 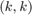 . Here, the number
. Here, the number 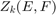 is referred to as the Zolotarev number.
is referred to as the Zolotarev number.
Again, for general sets  and
and 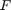 the solution to Zolotarev's third problem is not known explicitly; however, when
the solution to Zolotarev's third problem is not known explicitly; however, when ![$E = [-b,-1]$](example_zolotarev_eq05184243193873580565.png) and
and ![$F = [1,b]$](example_zolotarev_eq01389434467423910546.png) are intervals with
are intervals with 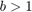 a closed-form expression is known. In fact, the third and fourth problem are mathematically equivalent (see [1, Sec. 51]). That is, the rational function that solves the fourth problem can be transformed to the solution of the third problem and vice versa. In particular, we have
a closed-form expression is known. In fact, the third and fourth problem are mathematically equivalent (see [1, Sec. 51]). That is, the rational function that solves the fourth problem can be transformed to the solution of the third problem and vice versa. In particular, we have
![$$\sup_{x\in [-b,-1]\cup [1,b]} | r(x) - {\rm sgn}(x) | = \frac{\sqrt{Z_k(E,F)}}{1+Z_k(E,F)},$$](example_zolotarev_eq14943458106459400253.png)
where ![$E = [-b,-1]$](example_zolotarev_eq05184243193873580565.png) and
and ![$F = [1,b]$](example_zolotarev_eq01389434467423910546.png) .
.
We can calculate ![$Z_k([-b,-1],[1,b])$](example_zolotarev_eq05769416934007763069.png) by using RKToolbox. First, we compute the approximation error between the sign function on
by using RKToolbox. First, we compute the approximation error between the sign function on ![$[-b,-1]\cup [1,b]$](example_zolotarev_eq00420577594769054965.png) and the rational approximation. Then, we solve the equation
and the rational approximation. Then, we solve the equation
![$$\sup_{[-b,-1]\cup [1,b]}| r(x) - {\mathrm sgn}(x) | = \frac{\sqrt{Z_k(E,F)}}{1+Z_k(E,F)} $$](example_zolotarev_eq05677563553261346248.png)
for 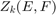 . That is,
. That is,
vals = 1-r(extrema); c = mean( vals(1:2:end) ); e = eig( [ 2-4/c^2 1 ; 1 0 ] ); Zk = min(abs(e))
Zk =
4.222581683574948e-07
To further verify the connection between the third and fourth Zolotarev problems we use a Mobius transform to convert the best rational approximation to 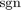 to the extremal rational function for
to the extremal rational function for 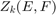 .
.
% Mobius transformation of r(x): R = @(x) (1 + (1+Zk)/(1-Zk)*r(x))./(1 - (1+Zk)/(1-Zk)*r(x)); x = linspace(-b, b, 5000); plot(x, R(x), 'linewidth', 2), ylim([-1e4,1e4]) xlabel('x') title('solution to Zolotarev''s third problem'), hold off
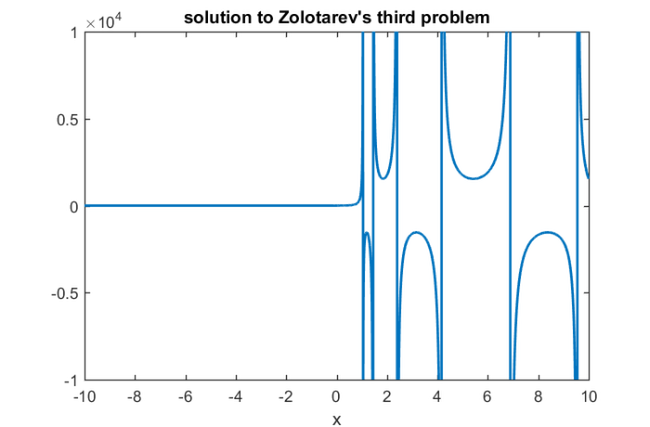
One can see that 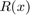 is such that
is such that 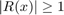 on
on 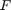 while being very small on
while being very small on  . We can verify that the rational function
. We can verify that the rational function 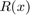 is the extremal rational function by checking that
is the extremal rational function by checking that  :
:
x = linspace(-b, -1, 1000); y = linspace(1, b, 1000); Zk max(abs(R(x))) / min(abs(R(y)))
Zk =
4.222581683574948e-07
ans =
4.222581683576213e-07
Nonsymmetric intervals: Sign approximation
RKToolbox does not directly construct the extremal rational functions to the third and fourth Zolotarev problems on real disjoint intervals that are not symmetric such as ![$[a,b]\cup [c,d]$](example_zolotarev_eq13849200424155012632.png) with either
with either  or
or 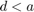 ; however, one can construct it by hand. First, one derives the Mobius transform that transplants
; however, one can construct it by hand. First, one derives the Mobius transform that transplants ![$[a,b]\cup [c,d]$](example_zolotarev_eq13849200424155012632.png) to symmetric intervals of the form
to symmetric intervals of the form ![$[-\gamma,-1]\cup [1,\gamma]$](example_zolotarev_eq07462347100810692974.png) with
with 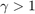 . This is only possible when
. This is only possible when  is selected so the cross-ratios of
is selected so the cross-ratios of 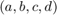 and
and 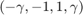 are equal. (Mobius transforms preserve the cross-ratio of collinear points.) Therefore, we know that
are equal. (Mobius transforms preserve the cross-ratio of collinear points.) Therefore, we know that  must satisfy
must satisfy
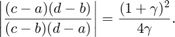
Here, is a graph that checks that the intervals (in blue) are mapped correctly to intervals of the form ![$[-\gamma,-1]\cup [1,\gamma]$](example_zolotarev_eq07462347100810692974.png) (in red) by the computed Mobius transform:
(in red) by the computed Mobius transform:
a = -10; b = -2; c = 1.1; d = 2*pi; % [a,b] \cup [c,d] cross = abs( (c-a)*(d-b)/(c-b)/(d-a) ); % | cross-ratio | gam = -1 + 2*cross + 2*sqrt(cross^2-cross); % preserve cross-ratio % Mobius transform: B = -(gam+1)*(d-c)/((gam-1)+ 2*(d-c)/(b-c)); A = -2*B/(b-c) - 1; C = 1; D = B; T = @(z) (A*z + (B - c*A))./(z+(D-c)); % Plot and check: x = [linspace(a,b) linspace(c,d)]; plot(x+1*1i,'.'), hold on, plot(T(x)+eps*1i, '.') xlim([-11 7]), ylim([-.5 1.5]) hold off
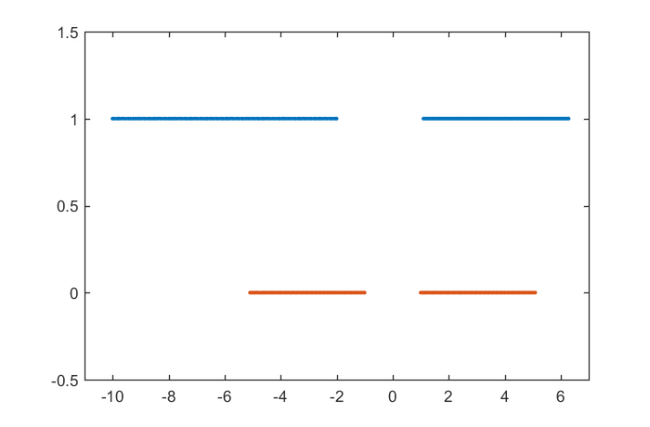
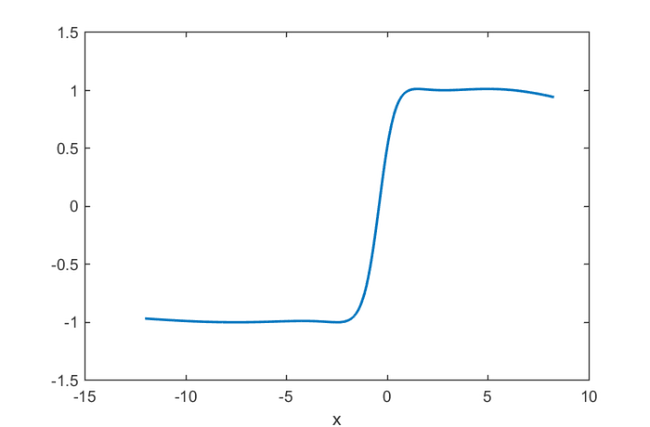
Composing the Mobius tranform with the best rational approximation to the sign function on ![$[-\gamma,-1]\cup [1,\gamma]$](example_zolotarev_eq07462347100810692974.png) derives the best rational approximation on
derives the best rational approximation on ![$[a,b]\cup [c,d]$](example_zolotarev_eq13849200424155012632.png) . Here, is the best rational approximation of degree
. Here, is the best rational approximation of degree 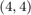 on
on ![$[-10, -2]\cup[1.1,2\pi]$](example_zolotarev_eq10391730016584358765.png) :
:
k = 4; r = rkfun.gallery('sign', k/2, gam); r = @(z) r( T(z) ); x = linspace(a-2,d+2,1000); plot(x, r(x), 'linewidth', 2) xlabel('x'), hold off
Other rational problems in RKToolbox
There are a selection of rational approximation problems that are closely related to Zolotarev's third and fourth problem in RKToolbox. We briefly mention them here as they are provided by the command rkfun.gallery.
Here is the best degree 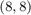 rational approximation to the unit step function on
rational approximation to the unit step function on ![$[-1,1]$](example_zolotarev_eq01893875229900969577.png) :
:
k = 8; r = rkfun.gallery('step', k/2); x = linspace(-5, 5, 1000); plot(x, r(x), 'k-', 'linewidth', 2) xlabel('x'), hold off title('best rational approximation to a step function')
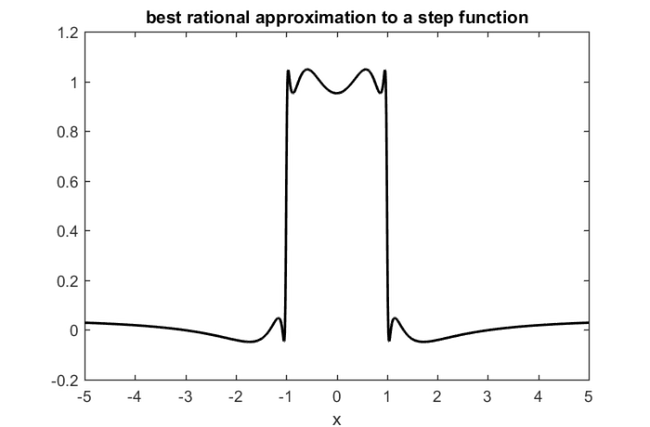
Here is the best degree  rational approximation to the sqrt function on
rational approximation to the sqrt function on ![$[1,10]$](example_zolotarev_eq11456966779805492727.png) :
:
k = 8; r = rkfun.gallery('sqrt', k/2, 10); x = linspace(1,10,1000); plot(x, 1 - sqrt(x)./r(x), 'k-', 'linewidth', 2) xlabel('x'), hold off title('error in best rational approx to sqrt')
Here is the best degree 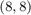 rational approximation to the inverse sqrt function on
rational approximation to the inverse sqrt function on ![$[1,10]$](example_zolotarev_eq11456966779805492727.png) :
:
k = 8; r = rkfun.gallery('invsqrt', k/2, 10); x = linspace(1,10,1000); plot(x, 1-r(x).*sqrt(x), 'k-', 'linewidth', 2) xlabel('x'), hold off title('error in best rational approx to invsqrt')
References
[1] N. I. Akhieser. Elements of the Theory of Elliptic Functions, Transl. of Math. Monographs 79, AMS, Providence RI (1990).
[2] B. Beckermann and A. Townsend. On the singular values of matrices with displacement structure, SIAM J. Matrix Anal. Appl., 38(4):1227--1248, 2017.
[3] S. Güttel, E. Polizzi, P. T. P. Tang, and G. Viaud. Zolotarev quadrature rules and load balancing for the FEAST eigensolver, SIAM J. Sci. Comput., 37(4):A2100--A2122, 2015.
[4] Y. Nakatsukasa and R. W. Freund. Computing fundamental matrix decompositions accurately via the matrix sign function in two iterations: The power of Zolotarev's functions, SIAM Review, 58:461--493, 2016.
[5] D. I. Zolotarev. Application of elliptic functions to questions of functions deviating least and most from zero, Zap. Imp. Akad. Nauk. St. Petersburg, 30:1--59, 1877.