Matching centrality measures for networks
Mary Aprahamian and Stefan Güttel, March 2016Download PDF or m-file
Contents
Introduction
The analysis of complex networks using tools from linear algebra has recently regained popularity. One way to define the relative importance of a network's node, known as centrality, is to quantify its ability to initiate walks around the network. The connection to linear algebra is that with each graph we can associate an adjacency matrix 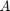 , so that
, so that 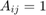 if there is an edge (either directed or undirected) from
if there is an edge (either directed or undirected) from  to
to 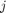 , and
, and 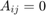 otherwise. The number of walks of length
otherwise. The number of walks of length  between nodes
between nodes  and
and 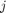 is obtained as the
is obtained as the 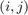 element of
element of 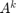 . The total number of walks originating from node
. The total number of walks originating from node  is the
is the  -th element of the vector
-th element of the vector 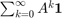 , where
, where 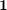 is the vector of all ones.
is the vector of all ones.
In applications it may be unreasonable to weigh very short and very long walks equally, so walks of length  are penalized by a parameter
are penalized by a parameter 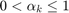 . Two choices of
. Two choices of 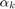 have been particularly popular:
have been particularly popular: 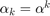 with
with 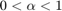 , and
, and 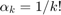 . In the former case we assume further that
. In the former case we assume further that 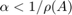 , where
, where 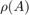 is the spectral radius of
is the spectral radius of 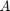 . In this case the vector centrality scores are the elements of
. In this case the vector centrality scores are the elements of 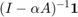 . This resolvent-based measure is known as Katz centrality [4]. In the second case the vector of centrality scores is
. This resolvent-based measure is known as Katz centrality [4]. In the second case the vector of centrality scores is 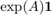 . This exponential-based measure is known as total communicability [2].
. This exponential-based measure is known as total communicability [2].
Depending on the application, either the exponential centrality or the resolvent centrality may be more appropriate to rank the importance of nodes, but also computational considerations may determine the choice of centrality. An interesting question is the following: for which value of the Katz parameter  will both centrality measures be most similar?
will both centrality measures be most similar?
This question is, of course, a simple rational approximation problem. For example, if we aim to minimize the 2-norm difference between the centrality vectors (allowing for some scaling), the problem becomes: find (real) parameters 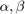 such that
such that
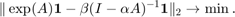
Note that if we are only interested in the ranking of nodes, the scaling of the resolvent centralities by 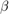 will have no effect on the ordering of the nodes.
will have no effect on the ordering of the nodes.
Power network example
We now demonstrate how RKFIT [3] can be used to determine good values for  and
and 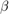 , a problem that is equivalent to finding a type
, a problem that is equivalent to finding a type 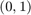 rational approximant
rational approximant 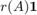 ,
, 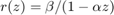 , of the exponential centrality
, of the exponential centrality 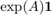 .
.
We consider a network arising as a topological representation of the Western States Power Grid of the USA. The network is available from the Florida Sparse Matrix collection (http://www.cise.ufl.edu/research/sparse/matrices/Newman/power.html). As a first step we load the adjacency matrix 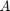 of the network and plot its associated graph:
of the network and plot its associated graph:
if exist('power.mat') ~= 2 disp('File power.mat not found. Can be downloaded from:') disp(['http://www.cise.ufl.edu/research/sparse/' ... 'matrices/Newman/power.html']) return end load power.mat A = Problem.A; G = graph(A, 'OmitSelfLoops'); plot(G, 'LineWidth', 1, 'EdgeColor', [0, 0, 0]); axis([-5.7, 7.5, -7, 6.5]), axis off
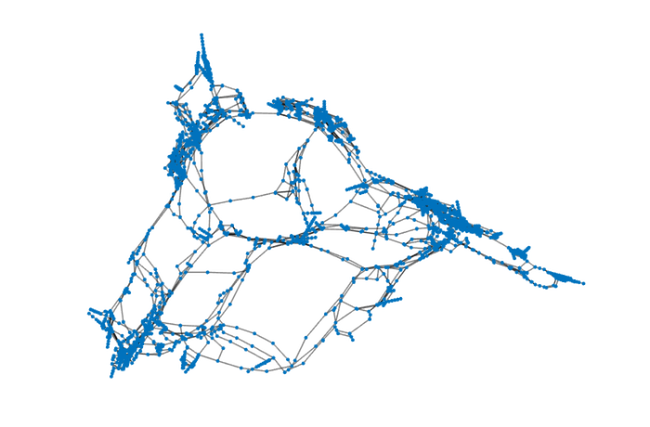
Exponential centrality
We now compute the exponential centralities using the function expmv available from http://www.mathworks.com/matlabcentral/fileexchange/29576-matrix-exponential-times-a-vector/content/expmv.m. By sorting the entries of the vector 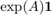 , we can identify the 10 highest ranked nodes in the power network:
, we can identify the 10 highest ranked nodes in the power network:
if exist('expmv') ~= 2 disp('Code exmpv not found. Can be downloaded from:') disp(['http://www.mathworks.com/matlabcentral/fileexchange/' ... '29576-matrix-exponential-times-a-vector/content/expmv.m']) return end b = ones(size(A, 1), 1); F = @(v) expmv(1, A, v); centr_exp = F(b); [~, ind_exp] = sort(centr_exp, 'descend'); disp(ind_exp(1:10))
4346
4382
4337
4333
4353
4396
4385
4374
4348
4403
Resolvent centrality
Now let us apply RKFIT for finding a Katz parameter  and the scaling
and the scaling  so that the resolvent-based centrality is closest to the exponential-based centrality in the 2-norm. The residue command allows us to easily convert the found ratfun into partial fraction form, which will have a single term here:
so that the resolvent-based centrality is closest to the exponential-based centrality in the 2-norm. The residue command allows us to easily convert the found ratfun into partial fraction form, which will have a single term here:
xi = inf; % initial guess for the pole param = struct('real', 1, 'maxit', 5, 'k', -1); [xi, ratfun, misfit] = rkfit(F, A, b, xi, param); [beta, xi] = residue(ratfun); alpha_rkfit = 1/xi;
Let us investigate the error of the type (0,1) best rational approximation to the exponential centrality vector of  as we vary the parameter
as we vary the parameter  . Note that, for given
. Note that, for given  , finding the optimal
, finding the optimal 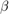 such that
such that 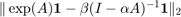 is smallest possible amounts to a linear least squares problem which we can solve by projection:
is smallest possible amounts to a linear least squares problem which we can solve by projection:
rhoA = eigs(A, 1); Alph = linspace(0.1, 1.05/rhoA, 500); for j = 1:length(Alph), res = (speye(size(A)) - Alph(j)*A)\b; res = res/norm(res); beta = res'*centr_exp; best_approx = beta*res; Dist(j) = norm(centr_exp - best_approx)/norm(centr_exp); end figure, plot(Alph, Dist, 'LineWidth', 1), hold on plot([alpha_rkfit, alpha_rkfit], [0, 1], 'r', 'LineWidth', 1) plot([1/rhoA, 1/rhoA], [0, 1], 'k--', 'LineWidth', 1) legend('best scaled resolvent', 'RKFIT parameter', ... '1/\rho(A)', 'Location', 'SouthWest') xlabel('Katz parameter \alpha'), axis tight
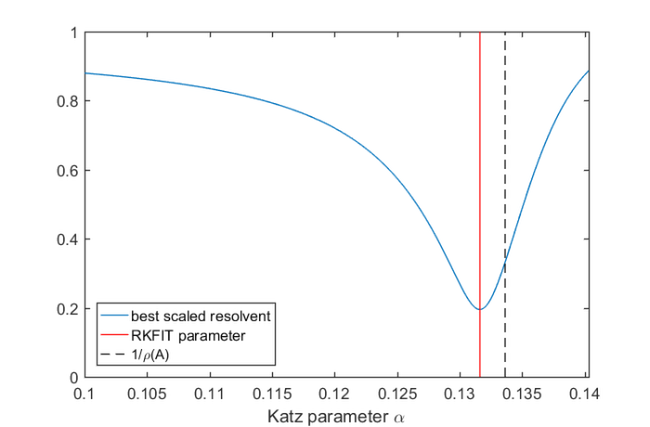
We note that RKFIT has done a very good job in locating the minimum, called 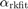 . Moreover, we find that
. Moreover, we find that 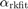 also satisfies the condition on the Katz parameter to be smaller than
also satisfies the condition on the Katz parameter to be smaller than 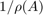 .
.
Another approach for choosing  has been suggested in [1]. There the aim was to minimize the distance between the two unscaled centrality vectors
has been suggested in [1]. There the aim was to minimize the distance between the two unscaled centrality vectors 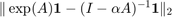 (i.e.,
(i.e., 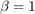 ). The authors recommend a value for the Katz parameter
). The authors recommend a value for the Katz parameter 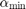 depending on the largest eigenvalue
depending on the largest eigenvalue 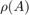 of the adjacency matrix,
of the adjacency matrix, 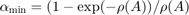 . For our power network the values
. For our power network the values 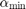 and
and 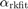 are very close:
are very close:
alpha_min = (1 - exp(-rhoA))/rhoA; disp([ alpha_min, alpha_rkfit ])
1.3356e-01 1.3162e-01
Here are the 15 highest ranked nodes using the exponential centrality measure and the resolvent centrality measures obtained using the parameters 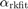 chosen by RKFIT and
chosen by RKFIT and 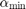 suggested in [1]:
suggested in [1]:
centr_rkfit = (speye(size(A)) - alpha_rkfit*A)\b; [~, ind_rkfit] = sort(centr_rkfit, 'descend'); centr_min = (speye(size(A))-alpha_min*A)\b; [~, ind_min] = sort(centr_min, 'descend'); [ (1:15)', ind_exp(1:15), ind_rkfit(1:15), ind_min(1:15) ]
ans =
1 4346 4382 4382
2 4382 4346 4346
3 4337 4337 4337
4 4333 4333 4333
5 4353 4353 4353
6 4396 4385 4385
7 4385 4403 4403
8 4374 4348 4348
9 4348 4396 4396
10 4403 4374 4374
11 4362 4362 4399
12 4399 4399 4362
13 4402 4402 4402
14 4414 4414 4414
15 4409 4409 4409
Both parameters provide a good resolvent-based match to the exponential centrality. In fact, the nodes ranked in the top 10 using the resolvent are the same with 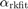 and
and 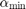 . The first difference between these two is in the 11-th and 12-th nodes which swap their positions when
. The first difference between these two is in the 11-th and 12-th nodes which swap their positions when 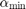 is used.
is used.
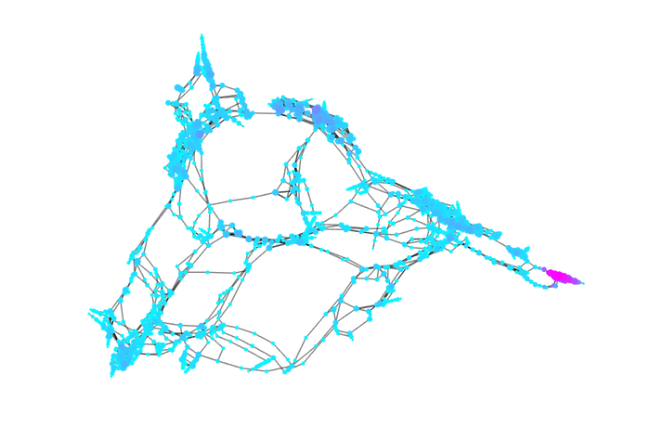
Finally, let us plot again the graph with the nodes being coloured according to the RKFIT-based centralities. Blue color indicates nodes of low centrality, and nodes with high centrality are plotted in magenta. The sizes of the nodes reflect their degrees.
figure deg = degree(G); plot(G, 'MarkerSize', 2*log(deg+1), ... 'NodeCData', log(centr_rkfit), ... 'LineWidth', 1, 'EdgeColor', [0, 0, 0]); colormap(cool) axis([-5.7, 7.5, -7, 6.5]), axis off
References
[1] M. Aprahamian, D. J. Higham, and N. J. Higham. Matching exponential-based and resolvent-based centrality measures, Journal of Complex Networks, 4(2):157--176, 2015.
[2] M. Benzi and C. Klymko. Total communicability as a centrality measure, Journal of Complex Networks, 1(2):124--149, 2013.
[3] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[4] L. Katz. A new status index derived from sociometric analysis, Psychometrika 18(1):39--43, 1953.