Computing with rational functions
Mario Berljafa and Stefan GüttelDownload PDF or m-file
Contents
Introduction
This toolbox comes with an implementation of a class called rkfun, which is the fundamental data type to represent and work with rational functions. Objects of this class are produced by the rkfit function (described in [2,3]), which in its simplest use case attemts to find a rational function  such that
such that
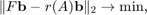
where 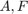 are square matrices and
are square matrices and 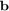 is a vector of compatible sizes. For example, let us consider
is a vector of compatible sizes. For example, let us consider 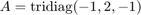 ,
, ![$\mathbf b = [1,0,\ldots,0]^T$](example_rkfun_eq00349232799794367251.png) , and
, and 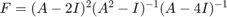 . We know that
. We know that 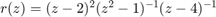 is a minimizer for the above problem. Let us try to find it via RKFIT:
is a minimizer for the above problem. Let us try to find it via RKFIT:
N = 100; A = gallery('tridiag', N); I = speye(N); F = (A - 4*I)\(A - 2*I)^2/(A^2 - I); b = eye(N,1); xi = inf(1, 5); [xi,ratfun,misfit] = rkfit(F, A, b, xi, 5, 1e-10, 'real');
As we started with 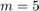 initial poles (at infinity), RKFIT will search for a rational function
initial poles (at infinity), RKFIT will search for a rational function  of type
of type 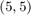 . When more than 1 iteration is performed and the tolerance tol is not chosen too small, RKFIT will try to reduce the type of the rational function while still maintaining a relative misfit below the tolerance, i.e.,
. When more than 1 iteration is performed and the tolerance tol is not chosen too small, RKFIT will try to reduce the type of the rational function while still maintaining a relative misfit below the tolerance, i.e., 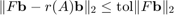 . Indeed, a reduction has taken place and the type has been reduced to
. Indeed, a reduction has taken place and the type has been reduced to 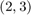 , as can be seen from the following output:
, as can be seen from the following output:
disp(ratfun)
RKFUN object of type (2, 3). Real-valued Hessenberg pencil (H, K) of size 4-by-3. coeffs = [-0.087, -0.394, -1.331, -1.503]
We can now perform various operations on the ratfun object, all implemented as methods of the class rkfun. To see a list of all methods just type help rkfun. We will now discuss some methods in more detail.
Evaluating an rkfun
We can easily evaluate 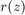 at any point (or many points) in the complex plane. The following command will evaluate
at any point (or many points) in the complex plane. The following command will evaluate  and
and 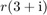 simultaneously:
simultaneously:
disp(ratfun([2; 3+1i]))
-1.2226e-14 + 0.0000e+00i 1.1765e-02 - 1.5294e-01i
We can also evaluate  as a matrix function, i.e., computing
as a matrix function, i.e., computing  for matrices
for matrices 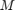 and
and 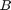 , by using two input arguments. For example, by setting
, by using two input arguments. For example, by setting  we effectively compute the full matrix function
we effectively compute the full matrix function  :
:
M = [3, 1; 0, 3]; B = eye(2); R = ratfun(M, B)
R =
-1.2500e-01 -2.8125e-01
0 -1.2500e-01
Plotting
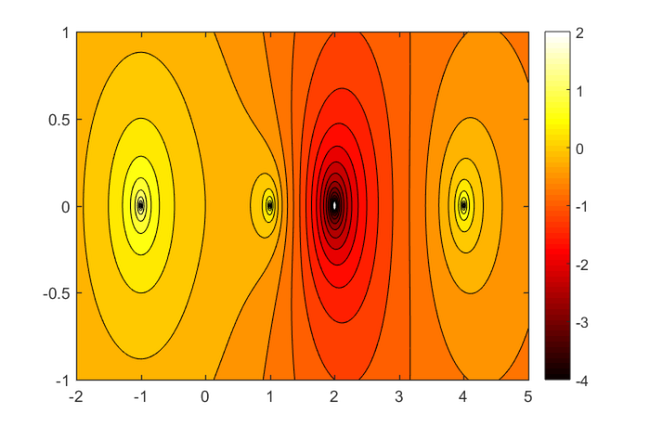
As  can be evaluated at any point in the complex plane, it is straightforward to produce plots of this function. For example, here is a contour plot of
can be evaluated at any point in the complex plane, it is straightforward to produce plots of this function. For example, here is a contour plot of 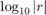 over the complex region
over the complex region ![$[-2,5]\times [-1,1]i$](example_rkfun_eq00501727816537830550.png) :
:
figure(1)
[X,Y] = meshgrid(-2:.01:5, -1:.01:1);
Z = X + 1i*Y;
R = ratfun(Z);
contourf(X, Y, log10(abs(R)), -4:.25:2)
colormap hot, colorbar
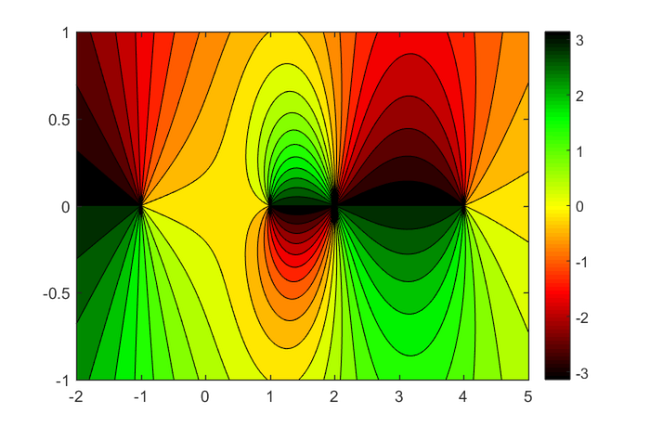
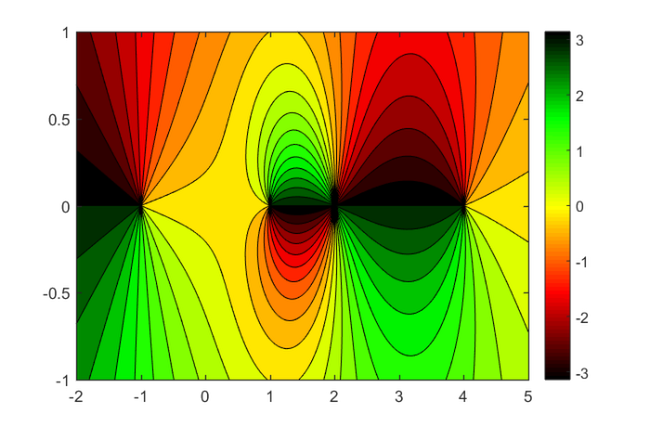
The following plot shows the phase portrait of  on the same domain. Can you spot the three poles and a double root?
on the same domain. Can you spot the three poles and a double root?
figure(3)
contourf(X, Y, angle(R), 20)
set(gca,'CLim',[-pi,+pi])
colormap(util_colormapc(1, 90));
colorbar
Another command ezplot can be used to get a quick idea of how ratfun looks over an interval on the real axis, in this case, ![$[-2,5]$](example_rkfun_eq02723052323934408023.png) :
:
figure(2)
ezplot(ratfun, [-2, 5])
ylim([-5, 5])
grid on
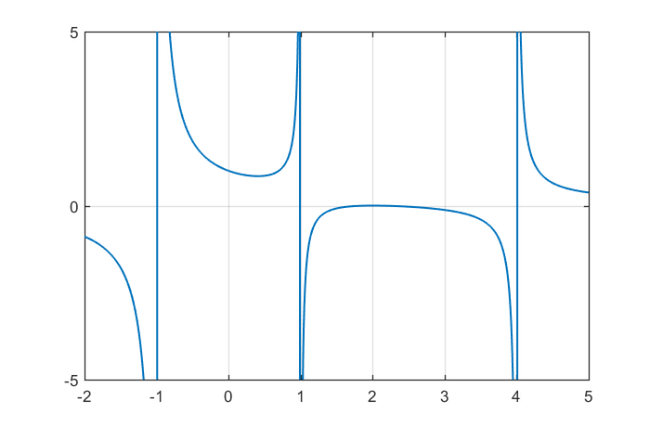
Pole- and root-finding
From the above plot we guess that  has poles at
has poles at  and
and 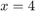 and a root at
and a root at 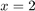 , which is to be expected from the definition of
, which is to be expected from the definition of  . The two commands poles and roots do exactly what their names suggest:
. The two commands poles and roots do exactly what their names suggest:
pls = poles(ratfun) rts = roots(ratfun)
pls = -1.0000e+00 1.0000e+00 4.0000e+00 rts = 2.0000e+00 + 2.7597e-07i 2.0000e+00 - 2.7597e-07i
As expected from a type (2,3) rational function, there are two roots and three poles. Note that the pole at 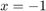 is identified with slightly less accuracy than the poles at
is identified with slightly less accuracy than the poles at 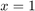 and
and 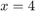 . This is because the point
. This is because the point 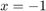 is outside the spectral interval of
is outside the spectral interval of 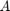 and hence sampled less accurately. Also the double root at
and hence sampled less accurately. Also the double root at  is identified up to an accuracy of
is identified up to an accuracy of  only. This is not surprising as the function is flat nearby multiple roots. However, the backward error of the roots is small:
only. This is not surprising as the function is flat nearby multiple roots. However, the backward error of the roots is small:
disp(ratfun(rts))
4.9960e-16 + 1.0588e-22i 4.9960e-16 - 1.0588e-22i
Basic arithmetic operations and differentiation
We have implemented some very basic operations for the rkfun class, namely, the multiplication by a scalar and the addition of a scalar. The result of such operations is again an rkfun object. For example, the following command computes points  where
where 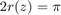 :
:
z = roots(2*ratfun - pi) disp(ratfun(z))
z = -4.0504e-01 8.5769e-01 1.5708e+00 1.5708e+00
We have currently not implemented the summation and multiplication of two rkfun objects, though this is doable in principle. ---UPDATE: This is no longer the case since Version 2.2 of the toolbox. Check out the example on "Electronic filter design using RKFUN arithmetic".--- However, we can already differentiate a rational function using the diff command. The following will find all real local extrema of  by computing the real roots of
by computing the real roots of 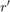 :
:
extrema = roots(diff(ratfun),'real')
extrema = 4.0759e-01 2.0000e+00
There are two real extrema which we can add to the above plot of  :
:
figure(2), hold on plot(extrema, ratfun(extrema), 'ro')

The syntax and "feel" of these computations is inspired by the Chebfun system [4], which represents polynomials via Chebyshev interpolants and allows for many more operations to be performed than our rkfun implementation. Here we are representing rational functions through their coefficients in a discrete-orthogonal rational function basis. Working with rational functions poses some challenges not encountered with polynomials. For example, the indefinite integral of a rational function is not necessarily a rational function but may contain logarithmic terms.
Multiple precision computations
Objects of class rkfun can be converted to MATLAB's Variable Precision Arithmetic (VPA) as follows:
disp(vpa(ratfun))
RKFUN object of type (2, 3). Real-valued Hessenberg pencil (H, K) of size 4-by-3. Variable precision arithmetic (VPA) activated. coeffs = [-0.087, -0.394, -1.331, -1.503]
Alternatively, we can also use the Advanpix Multiple Precision (MP) toolbox [1], which is typically more efficient and reliable than VPA. We recommend the use of this toolbox in particular for high-precision root-finding of rkfun's and conversion to partial fraction form:
ratfun = mp(ratfun)
ratfun = RKFUN object of type (2, 3). Real-valued Hessenberg pencil (H, K) of size 4-by-3. Multiple precision arithmetic (ADVANPIX) activated. coeffs = [-0.087, -0.394, -1.331, -1.503]
When evaluating a multiple precision ratfun, the result will be returned in multiple precision:
format longe
ratfun(2)
ans =
-1.2125294919816719385880796519441591e-14
It is important to understand that, although the evaluation of ratfun is now done in multiple precision, the computation of ratfun using the rkfit command has been performed in standard double precision. rkfit does not currently support the computation of rkfun objects in multiple precision. Here are the roots of ratfun computed in multiple precision:
roots(ratfun)
ans =
Columns 1 through 1
2.00000000000005884325215506037004691e+00 + 2.69725359428640320019961191862469502e-07i
2.00000000000005884325215506037004691e+00 - 2.69725359428640320019961191862469502e-07i
Conversion to partial fraction form
It is often convenient to convert a rational function  into its partial fraction form
into its partial fraction form
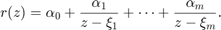
The residue command of our toolbox performs such a conversion. Currently, this only works when the poles  of
of  are distinct and
are distinct and  is not of superdiagonal type (i.e., there is no linear term in
is not of superdiagonal type (i.e., there is no linear term in  ). As the conversion to partial fraction form can be an ill-conditioned transformation, we recommend to use residue in conjunction with the multiple precision feature. Here are the poles
). As the conversion to partial fraction form can be an ill-conditioned transformation, we recommend to use residue in conjunction with the multiple precision feature. Here are the poles  and residues
and residues 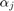 (
( ), as well as the absolute term
), as well as the absolute term 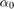 , of the function
, of the function  defined above:
defined above:
[alpha, xi, alpha0, cnd] = residue(mp(ratfun)); double([xi , alpha]) double(alpha0)
ans =
-9.999999999999628e-01 8.999999999998803e-01
9.999999999999993e-01 -1.666666666666714e-01
3.999999999999999e+00 2.666666666666091e-01
ans =
-1.749809464778146e-17
The absolute term is close to zero because  is of subdiagonal type. The output cnd of residue corresponds to the condition number of the transformation to partial fraction form. In this case of a low-order rational function with well separated poles the condition number is actually quite moderate:
is of subdiagonal type. The output cnd of residue corresponds to the condition number of the transformation to partial fraction form. In this case of a low-order rational function with well separated poles the condition number is actually quite moderate:
cnd
cnd =
5.615057038451497e+01
Conversion to quotient and continued fraction form
Our toolbox also implements the conversion of a rkfun to quotient form 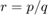 with two polynomials
with two polynomials  and
and 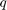 given in the monomial basis. As with the conversion to partial fraction form, we recommend performing this transformation in multiple precision arithmetic due to potential ill-conditioning. Here we convert
given in the monomial basis. As with the conversion to partial fraction form, we recommend performing this transformation in multiple precision arithmetic due to potential ill-conditioning. Here we convert  into the
into the  form and evaluate it at the root
form and evaluate it at the root 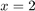 using MATLAB's polyval command:
using MATLAB's polyval command:
[p,q] = poly(double(ratfun)); polyval(p, 2)./polyval(q, 2)
ans =
-1.273055734903527e-14
A rkfun can also be converted into continued fraction form
$$ \displaystyle r(z) = h_0 + \cfrac{1}{\hat h_1+\cfrac{1}{h_1+\cfrac{1}{\hat h_2+\cdots+\cfrac{1}{h_{m-1}+\cfrac{1}{\hat h_m z+\cfrac{1}{h_m}}}}}} $$
as follows:
[h, hhat, absterm, cnd] = contfrac(mp(ratfun));
That's it for this tutorial. Note that more methods will be added over time and we'd be happy to receive any feedback or bug reports. For more details about the internal representation of rkfun, see [3].
The following command creates a thumbnail.
figure(3), hold on, plot(NaN)
References
[1] Advanpix LLC., Multiprecision Computing Toolbox for MATLAB, ver 4.3.3.12213, Tokyo, Japan, 2017. http://www.advanpix.com/.
[2] M. Berljafa and S. Güttel. Generalized rational Krylov decompositions with an application to rational approximation, SIAM J. Matrix Anal. Appl., 36(2):894--916, 2015.
[3] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[4] T. A. Driscoll, N. Hale, and L. N. Trefethen. Chebfun Guide, Pafnuty Publications, Oxford, 2014. http://www.chebfun.org