Moving the poles of a rational Krylov space
Mario Berljafa and Stefan Güttel, June 2015Download PDF or m-file
Contents
Rational Krylov spaces
A rational Krylov space is a linear vector space of rational functions in a matrix times a vector [5]. Let 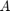 be a square matrix of size
be a square matrix of size 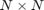 ,
, 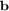 an
an 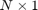 nonzero starting vector, and let
nonzero starting vector, and let  be a sequence of complex or infinite poles all distinct from the eigenvalues of
be a sequence of complex or infinite poles all distinct from the eigenvalues of 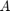 . Then the rational Krylov space of order
. Then the rational Krylov space of order 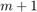 associated with
associated with 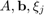 is defined as
is defined as
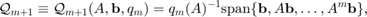
where 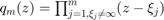 is the common denominator of the rational functions associated with
is the common denominator of the rational functions associated with 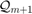 . The rational Krylov sequence method by Ruhe [5] computes an orthonormal basis
. The rational Krylov sequence method by Ruhe [5] computes an orthonormal basis 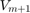 of
of 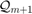 . The first column of
. The first column of 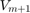 can be chosen as
can be chosen as 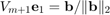 . The basis matrix
. The basis matrix 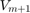 satisfies a rational Arnoldi decomposition of the form
satisfies a rational Arnoldi decomposition of the form
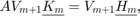
where 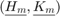 is an (unreduced) upper Hessenberg pencil of size
is an (unreduced) upper Hessenberg pencil of size 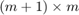 .
.
The poles of a rational Krylov space
Given a rational Arnoldi decomposition of the above form, it can be shown [1] that the poles 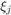 of the associated rational Krylov space are the generalized eigenvalues of the lower
of the associated rational Krylov space are the generalized eigenvalues of the lower 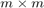 subpencil of
subpencil of 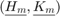 . Let us verify this at a simple example by first constructing a rational Krylov space associated with the
. Let us verify this at a simple example by first constructing a rational Krylov space associated with the 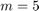 poles
poles 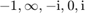 . The matrix
. The matrix 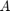 is of size
is of size 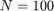 and chosen as the tridiag matrix from MATLAB's gallery, and
and chosen as the tridiag matrix from MATLAB's gallery, and 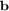 is the first canonical unit vector. The rat_krylov command is used to compute the quantities in the rational Arnoldi decomposition:
is the first canonical unit vector. The rat_krylov command is used to compute the quantities in the rational Arnoldi decomposition:
N = 100;
A = gallery('tridiag', N);
b = eye(N, 1);
m = 5;
xi = [-1, inf, -1i, 0, 1i];
[V, K, H] = rat_krylov(A, b, xi);
Indeed, the rational Arnoldi decomposition is satisfied with a residual norm close to machine precision:
format shorte
disp(norm(A*V*K - V*H) / norm(H))
3.5143e-16
And the chosen poles 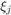 are the eigenvalues of the lower
are the eigenvalues of the lower 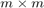 subpencil:
subpencil:
disp(eig(H(2:m+1,1:m),K(2:m+1,1:m)))
-1.0000e+00 + 0.0000e+00i
Inf + 0.0000e+00i
0.0000e+00 - 1.0000e+00i
0.0000e+00 + 0.0000e+00i
0.0000e+00 + 1.0000e+00i
Moving the poles explicitly
There is a direct link between the starting vector 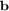 and the poles
and the poles 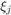 of a rational Krylov space
of a rational Krylov space 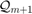 . A change of the poles
. A change of the poles 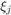 to
to  can be interpreted as a change of the starting vector from
can be interpreted as a change of the starting vector from 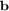 to
to 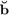 , and vice versa. Algorithms for moving the poles of a rational Krylov space are described in [1] and implemented in the functions move_poles_expl and move_poles_impl.
, and vice versa. Algorithms for moving the poles of a rational Krylov space are described in [1] and implemented in the functions move_poles_expl and move_poles_impl.
For example, let us move the poles of the above rational Krylov space 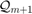 to the points
to the points  :
:
xi_new = -1:-1:-5; [KT, HT, QT, ZT] = move_poles_expl(K, H, xi_new);
The output of move_poles_expl are unitary matrices 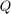 and
and 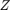 , and transformed upper Hessenberg matrices
, and transformed upper Hessenberg matrices 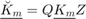 and
and 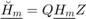 , so that the lower
, so that the lower 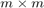 part of the pencil
part of the pencil 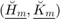 has as generalized eigenvalues the new poles
has as generalized eigenvalues the new poles  :
:
disp(eig(HT(2:m+1,1:m),KT(2:m+1,1:m)))
-1.0000e+00 + 0.0000e+00i -2.0000e+00 + 1.4085e-15i -3.0000e+00 - 7.2486e-16i -4.0000e+00 + 1.6407e-16i -5.0000e+00 - 2.4095e-16i
Defining 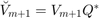 , the transformed rational Arnoldi decomposition is
, the transformed rational Arnoldi decomposition is
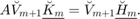
This can be verified numerically by looking at the residual norm:
VT = V*QT'; disp(norm(A*VT*KT - VT*HT) / norm(HT))
6.8004e-16
It should be noted that the function move_poles_expl can be used to move the  poles to arbitrary locations, including to infinity, and even to the eigenvalues of
poles to arbitrary locations, including to infinity, and even to the eigenvalues of 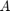 . In latter case, the transformed space
. In latter case, the transformed space 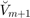 does not correspond to a rational Krylov space generated with starting vector
does not correspond to a rational Krylov space generated with starting vector  and poles
and poles  , but must be interpreted as a filtered rational Krylov space. Indeed, the pole relocation problem is very similar to that of applying an implicit filter to the rational Krylov space [3,4]. See also [1] for more details.
, but must be interpreted as a filtered rational Krylov space. Indeed, the pole relocation problem is very similar to that of applying an implicit filter to the rational Krylov space [3,4]. See also [1] for more details.
Moving the poles implicitly
Assume we are given a nonzero vector 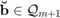 with coefficient representation
with coefficient representation 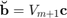 , where
, where  is a vector with
is a vector with 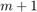 entries. The function move_poles_impl can be used to obtain a transformed rational Arnoldi decomposition with starting vector
entries. The function move_poles_impl can be used to obtain a transformed rational Arnoldi decomposition with starting vector 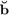 .
.
As an example, let us take ![$\mathbf{c} = [0,\ldots,0,1]^T$](example_move_poles_eq13853633333888533310.png) and hence transform the rational Arnoldi decomposition so that
and hence transform the rational Arnoldi decomposition so that 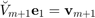 , the last basis vector in
, the last basis vector in 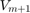 :
:
c = zeros(m+1,1); c(m+1) = 1; [KT, HT, QT, ZT] = move_poles_impl(K, H, c); VT = V*QT';
The poles of the rational Krylov space with the modified starting vector can again be read off as the generalized eigenvalues of the lower 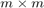 part of
part of 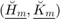 :
:
disp(eig(HT(2:m+1,1:m),KT(2:m+1,1:m)))
3.2914e+00 - 5.5756e-02i 1.8705e+00 - 1.2100e-01i 7.7852e-01 - 9.2093e-02i 1.9752e-01 - 3.0824e-02i 4.4392e-03 - 3.5884e-04i
This implicit pole relocation procedure is key element of the RKFIT algorithm described in [1,2].
Some fun with moving poles
To conclude this example, let us consider a 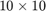 random matrix
random matrix 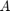 , a random vector
, a random vector 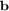 , and the corresponding
, and the corresponding 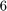 -dimensional rational Krylov space with poles at
-dimensional rational Krylov space with poles at 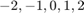 :
:
A = (randn(10) + 1i*randn(10))*.5; b = randn(10,1) + 1i*randn(10,1); m = 5; xi = -2:2; [V, K, H] = rat_krylov(A, b, xi);
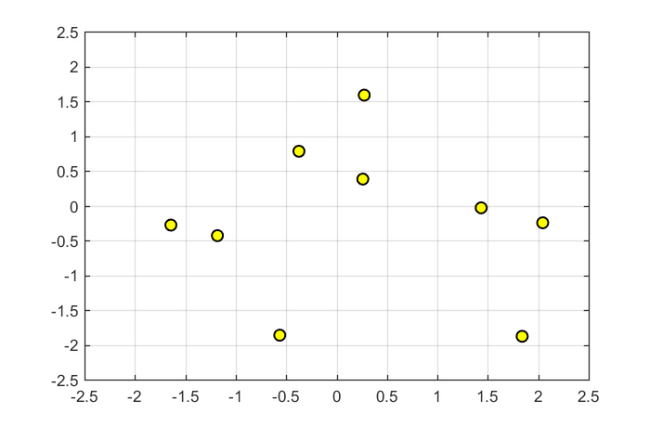
Here are the eigenvalues of 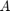 :
:
figure plot(eig(A),'ko','MarkerFaceColor','y') axis([-2.5,2.5,-2.5,2.5]), grid on, hold on
We now consider a  -dependent coefficient vector
-dependent coefficient vector 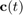 such that
such that 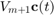 is continuously "morphed" from
is continuously "morphed" from 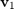 to
to 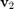 . The poles of the rational Krylov space with the transformed starting vector
. The poles of the rational Krylov space with the transformed starting vector 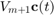 are then plotted as a function of
are then plotted as a function of  .
.
for t = linspace(1,2,51), c = zeros(m+1,1); c(floor(t)) = cos(pi*(t-floor(t))/2); c(floor(t)+1) = sin(pi*(t-floor(t))/2); [KT, HT, QT] = move_poles_impl(K, H, c);% transformed pencil xi_new = sort(eig(HT(2:m+1,1:m),KT(2:m+1,1:m))); % new poles plot(real(xi_new), imag(xi_new), 'b+') end
As one can see, only one of the five poles starts moving away from  , with the remaining four poles staying at their positions. This is because "morphing" the starting vector from
, with the remaining four poles staying at their positions. This is because "morphing" the starting vector from  to
to 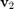 only affects a two-dimensional subspace of
only affects a two-dimensional subspace of 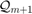 which includes the vector
which includes the vector 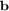 and is itself a rational Krylov space, and this space is parameterized by one pole only.
and is itself a rational Krylov space, and this space is parameterized by one pole only.
As we now continue morphing from 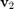 to
to 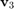 , another pole starts moving:
, another pole starts moving:
for t = linspace(2,3,51), c = zeros(m+1,1); c(floor(t)) = cos(pi*(t-floor(t))/2); c(floor(t)+1) = sin(pi*(t-floor(t))/2); [KT, HT, QT, ZT] = move_poles_impl(K, H, c); xi_new = sort(eig(HT(2:m+1,1:m),KT(2:m+1,1:m))); plot(xi_new, 'r+') end
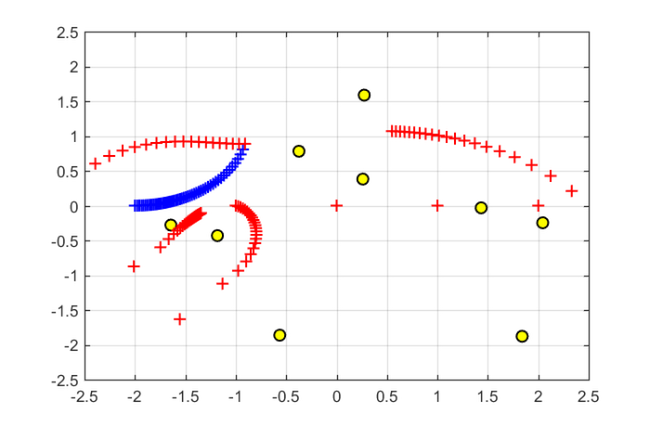
Morphing from 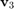 to
to 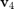 , then to
, then to 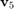 , and finally to
, and finally to 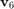 will eventually affect all five poles of the rational Krylov space:
will eventually affect all five poles of the rational Krylov space:
for t = linspace(3, 5.99, 150) c = zeros(m+1,1); c(floor(t)) = cos(pi*(t-floor(t))/2); c(floor(t)+1) = sin(pi*(t-floor(t))/2); [KT, HT, QT, ZT] = move_poles_impl(K, H, c); xi_new = sort(eig(HT(2:m+1, 1:m), KT(2:m+1, 1:m))); switch floor(t) case 3, plot(xi_new', 'g+') case 4, plot(xi_new', 'm+') case 5, plot(xi_new', 'c+') end end
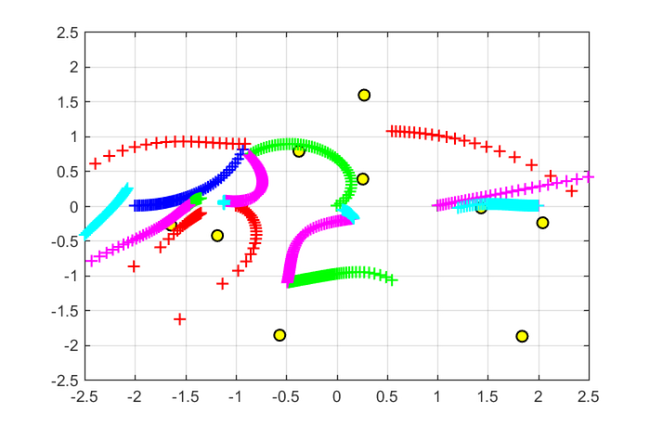
References
[1] M. Berljafa and S. Güttel. Generalized rational Krylov decompositions with an application to rational approximation, SIAM J. Matrix Anal. Appl., 36(2):894--916, 2015.
[2] M. Berljafa and S. Güttel. The RKFIT algorithm for nonlinear rational approximation, SIAM J. Sci. Comput., 39(5):A2049--A2071, 2017.
[3] G. De Samblanx and A. Bultheel. Using implicitly filtered RKS for generalised eigenvalue problems, J. Comput. Appl. Math., 107(2):195--218, 1999.
[4] G. De Samblanx, K. Meerbergen, and A. Bultheel. The implicit application of a rational filter in the RKS method, BIT, 37(4):925--947, 1997.
[5] A. Ruhe. Rational Krylov: A practical algorithm for large sparse nonsymmetric matrix pencils, SIAM J. Sci. Comput., 19(5):1535--1551, 1998.